Формулы объема геометрических фигур, труб

Разновидности фундамента и кубатура

• столбчатый;
• ленточный;
• плитный.

Очевидно, расчет кубатуры в каждом отдельном случае индивидуален. Начнем со столбчатого фундамента:

1. Рассчитываем объем железобетонных опор (каждой по отдельности). Для этого перемножаем между собой ее стороны и высоту элемента основания.
2. В случае круглого сечения столбиков умножаем квадрат их радиуса на число элементов.
3. Результат умножаем на показатель высоты опоры.
4. Полученное число умножаем на число необходимых для сооружения фундамента столбов. В итоге получим общий объем бетона.
5. В случае связки элементов основания бетонным ростверком необходимо воспользоваться формулой параллелепипеда и рассчитать его объем.

При расчете кубатуры ленточного фундамента для начала определяем его сечение. Если оно ровное, трудностей с расчетом кубатуры возникнуть не должно. В этом случае умножаем периметр конструкции на ее толщину и ширину. Далее, следуем инструкции по расчету:

• например, имеем конструкцию со сторонами 10*10 метров. Ширина основания — 0.4 метра, толщина — 0.7 метра;
• следовательно, периметр сооружения равен 40 метров (10*4). После перемножения величин получаем 11.2 метра. Однако это только показатель объема основания для стен снаружи;
• допустим, дом имеет две перегородки (длина одной из них — 10 метров, длина перпендикулярной первой — 5 метров, ширина обеих составляет 0.3 метра, толщина — 0.7 метра);
• перемножаем параметры одного из участков (10*0.3*0.7=2.1), затем второго (5*0.3*0.7=1.05). Далее, просто складываем полученные значения и получаем общий объем бетона, необходимого для устройства ленточного фундамента (11.2+2.1+1.05=14.35 м3).

Кубатура плитного фундамента вычисляется наиболее просто. Чтобы определить кубатуру плитного основания потребуется лишь перемножить показатели длины, ширины и толщины плиты.

Например, имеет следующие данные: 10, 0.4 и 10 метров. Вычисляем объем, перемножая показатели, и получаем 40 м3 — объем необходимого бетона.

Однако следует учесть, что в целях повышения прочности плитного фундамента нередко прибегают к оснащению плит ребрами жесткости. Если вы имеете дело именно с таким проектом, для того, чтобы рассчитать необходимое количество материала, нужно вычислить отдельно объем плиты и ребер и сложить полученные значения.

Итак, показатель, связанный с плитой мы уже знаем. Осталось подсчитать кубатуру ребер жесткости.

Допустим, в нашем случае основание имеет четыре усиленных элемента с показателями 10, 0.25 и 0.3 метра. Очевидно, объем одного ребра жесткости — 0.75 метра. Общий показатель для всех ребер равен 3-м кубометрам (0.75*4). Затем для вычисления общего количества раствора, необходимого для устройства плитного фундамента, нужно сложить полученные значения (40+3) и получим 43 м³.

Расчет кубатуры помещения

Если интересующее вас помещение имеет несложную форму, то рассчитать его кубатуру совсем нетрудно: просто перемножьте показатели ширины, длины и высоты помещения.

Если вы не располагаете одной или несколькими характеристиками помещения, измерьте их с помощью рулетки или дальномера. С целью повышения точности проводимых измерений можете замерять высоту и ширину противоположных стен по два раза, затем сложить и разделите полученное значение пополам (найдите среднее арифметическое).

Допустим, вам известна площадь помещения. Чтобы найти кубатуру необходимо этот показатель умножить на высоту.

Если же помещение имеет непростую форму, для начала условно разделите помещение на простые фигуры и, воспользовавшись геометрическими формулами, вычислите объем каждой из них, затем сложите значения.

Расчет кубатуры из массы

Если известна масса вещества, для которого необходимо рассчитать объем (кубатуру), следует для начала уточнить плотность этого вещества. Этот показатель можно измерить самостоятельно или же узнать в таблице плотности веществ.

Для того чтобы узнать количество кубических метров, следует разделить известный нам показатель массы вещества на его плотность. При этом масса измеряется в килограммах, а плотность в кг/м3.

Перевод в другие единицы

Для перевода в необходимое значение надо помнить довольно простые пропорции перевода метров в сантиметры и миллиметры.

Единицы длины:

1 м = 100 см = 1 000 мм

Единицы площади:

1 м² = 10 000 см² = 1 000 000 мм²

Единицы объема:

1 м³ = 1 000 000 см³ = 1 000 000 000 мм³

Количество жидкости очень часто измеряется в литрах, тут достаточно знать, что:

• 1 л = 1 000 см³
• 1 000 л = 1 м³

Довольно часто приходится рассчитывать объем, исходя из веса, и тут нужно знать плотность вещества. Проще всего с водой, плотность которой 1т/1м³. То есть тонна воды займет один м³ (куб), а тонна молока, например, займет примерно 1,030 куба.

Песок имеет плотность от 1,3 т/м³ до 1,8 т/м³. Это значит, что один м³ весит от 1,3 до 1,8 тонны.

Расчет кубатуры пиломатериалов имеет тонкости. Если доска обрезная и одинаковая, достаточно взять одну, измерить длину, толщину, ширину, перемножить эти параметры, а затем получившееся значение умножить на общее количество. Это и будет искомое значение.

Бывает также, что приходится высчитывать вместимость цилиндрических объектов (бочек, цистерн и подобных). Основанием здесь служит круг, а площадь его равна произведению числа пи (π = 3.14) на квадрат радиуса (половины диаметра) или S=πR².

В практической жизни можно применить и такой достаточно простой способ определения объема жидкостей или сыпучих веществ — в кубометре содержится 1 тыс. литров или 100 десятилитровых ведер. Кому-то покажется хлопотным таскать и пересчитывать ведра с песком или водой, но этот способ точен и общедоступен.

Пример расчета

Допустим, нужно залить ленточный фундамент под сооружение размером 8 на 12 метров, разделенное на три помещения стенами длиной 8 и 6 метров. Примем ширину фундамента 40 см, высоту в метр. Длина составит 54 метра, а объем фундамента будет 0,4*1*54 = 21,6 м³. Это значение можно смело округлить до 22 м³.

Приготовление кубометра бетонной смеси для заливки фундамента требует примерно 350 кг цемента, 800 кг песка, 1200 кг щебня и 140 л воды. Значит, на весь фундамент нужно 154 мешка цемента по 50 кг (7,7 тонн), 17,6 тонн песка, 26,4 тонн щебня и примерно 3 кубометра воды.

Это совершенно приблизительный подсчет, навскидку, позволяющий просто прикинуть размер предстоящих материальных и трудовых затрат. Кстати, количество вынутого под фундамент грунта будет сопоставимо, а то и выше объема самого фундамента, хотя тот и не полностью находится в земле. Объясняется это тем, что траншея под фундамент роется шире для установки опалубки и сопутствующих работ.

Точно так же приходится рассчитывать потребный объем при, допустим, переезде или отправке каких-то товаров или грузов. Ведь переплачивать за лишний объем кузова заказанного автомобиля, транспортного контейнера или железнодорожного вагона никому не хочется.

Достаточно просто вспомнить (посмотреть в интернете) элементарные геометрические формулы из школьной программы и приложить здравый смысл. Ведь всегда можно приблизительно рассчитать объем мебели при переезде или коробок при отправке товара и оценить предстоящие усилия и затраты. А для более точных, окончательных расчетов всегда можно прибегнуть к помощи специалистов. Тем более что предварительный итог более или менее известен, и это может служить некоторой проверкой при согласовании условий.

Как определить вместимость сосудов разных форм

Вычисление объема параллелепипеда

Параллелепипед — это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.

\(V = S_{осн} \times H. \)

Прямоугольный параллелепипед — это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, — это куб.

Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
 

\(V = AB \times AD \times AA_{1} = abc.\)
Объем куба равен кубу его стороны:\(V = a^{3}.\)

Нахождение объема пирамиды

Пирамида — это многогранник, состоящий из основания — плоского многоугольника, вершины — точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды — это перпендикуляр, опущенный из вершины на плоскость основания.

\(V = \frac{1}{3} \times S_{осн} \times h.\)

Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований — \(S_{1}\) и \(S_{2}\).

\(V = \frac{1}{3} \times h \times (S_{1} + S_{2} + \sqrt{S_{1} \times S_{2}}). \)

Как найти объем цилиндра

Цилиндр — это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

\(R\) — радиус основания цилиндра, \(h\) — его высота, равная образующей оси.\(V = S_{осн} \times h = \pi \times R^{2} \times h.\)

Если нужно найти объем усеченного цилиндра, то понадобится не только R — радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l — \(l_{1}\) и  \(l_{2}\).\(V = \pi \times R^{2} \times \frac{l_{1} + l_{2}}{2}.\)

Как высчитать объем конуса

Конус — это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.

\(V = \frac{1}{3} \times S_{осн} \times h = \frac{1}{3} \times \pi \times R^{2} \times h.\)

Чтобы найти объем усеченного конуса, понадобятся \(R_{1}\) и \(R_{2}\) — радиусы оснований, а также высота \(h\).

\(V = \frac{\pi \times h}{3} \times (R_1^2 + R_2^2 + R_1 \times R_2).\)

Нахождение объема шара

Шар — это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.

Готовимся определить объем бетона – как посчитать без ошибок

Готовясь к выполнению расчетов, следует запомнить, что потребность в бетонной смеси определяется в кубометрах, а не в килограммах, тоннах или литрах. В результате ручных или программных расчетов будет определен объем связующего раствора, а не его масса. Одна из главных ошибок, которую допускают начинающие застройщики – выполнение расчетов до того, как будет определен тип фундаментной основы.

Решение о конструкции фундамента принимается после выполнения следующих работ:

• производства геодезических мероприятий, позволяющих определить свойства грунта, уровень замерзания и расположение водоносных жил;
• вычисления нагрузочной способности базы. Она определяется на основании веса, конструктивных особенностей строения и природных факторов.

Как рассчитать количество (объем) бетонной смеси

Легко рассчитать объем бетона, используя специальную программу или онлайн-калькулятор, которые учитывают множество факторов:

• разновидность сооружаемой основы;
• габариты фундамента, его конфигурацию;
• марку смеси, применяемую для бетонирования;
• глубину промерзания грунта.

Точность, с которой посчитан объем бетона, зависит от используемых для расчета данных.

Они разные для каждого типа фундамента:

при расчете ленточного основания учитываются его габариты и форма;
для столбчатой основы важно знать количество бетонных колонн и их размеры;
рассчитать куб бетона для цельной плиты можно по ее толщине и размерам.

От полноты используемых для расчета данных зависит точность полученного результата.

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.

Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a * b * h

Подставляем наши числа:

V = 18 * 10 * 7 = 1260 см3.

Ответ: объём параллелепипеда = 1260 см3.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём = 120 см3, а высота — 15 см.

Как решаем:

V = 120 см3

h = 15 см

V = S осн * h

S осн = V : h

S осн = 120 см3: 15 см = 8 см2.

Ответ: площадь основания параллелепипеда = 8 см2.

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания = 30 сантиметров, ширина = 12 см, а высота = 5 см.

Как решаем:

S п.п. = 2 (ab + ac + bc)

S п.п. = 2(30 * 12 + 30 *5 + 12 * 5) = 2 * (360 + 150 + 60) = 2 * 570 = 1140 см2.

Ответ: площадь полной поверхности параллелепипеда = 1140 см2.

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.

V параллелепипеда	V = a * b * h
	V = S осн * h
S боковой поверхности	S б.п. = 2(ac + bc)
S полной поверхности	S п.п. = 2 (ab + ac + bc)
Диагональ параллелепипеда	d2 = a2+ b2 + c2

Шаги

Метод 1 из 2:

Вычисление объема прямоугольного предмета (в кубических сантиметрах)

1. 1

   Измерьте длину, ширину и высоту предмета (в сантиметрах). Для этого измерьте требуемые величины с помощью линейки или рулетки или конвертируйте известные вам значения в сантиметры.
   X
   Источник информации

   Например, если вы хотите узнать объем холодильника, найдите его длину, ширину и высоту (в сантиметрах). Предположим, что ваш холодильник в высоту имеет 100 см, в ширину — 50 см, в длину — 40 см.

2. 2

   Запишите высоту предмета.

   В нашем примере запишите, что высота = 100 см.

   Вы можете перемножать величины в любом порядке. Например, начните с высоты.

3. 3

   Умножьте высоту на ширину. Затем умножьте первую величину на какую-нибудь из оставшихся (любую). Например, умножьте высоту на ширину.
   X
   Источник информации

   В нашем примере, умножьте 100 на 50: 100 × 50 = 5000.

4. 4

   Умножьте полученный результат на длину предмета.

   В нашем примере, умножьте 5000 на 40: 5000 × 40 =Н 200 000.

   Последний шаг — умножьте полученный результат на оставшуюся величину. Например, умножьте произведение высоты и ширины на длину.

5. 5

   Запишите ответ в кубических сантиметрах, чтобы он был понятен любому человеку.

   • Единицы измерения записываются так:
     • кубические сантиметры
     • сантиметров в кубе
     • см^3
     • см3

Метод 2 из 2:

Вычисление объема других фигур

1. 1

   Объем куба V= L3, где V — объем, L — сторона. Куб — прямоугольный параллелепипед, у которого все стороны равны.
   X
   Источник информации

   Таким образом, формулу для вычисления объема куба можно записать в виде: длина × ширина × глубина = длина × длина × длина = длина3. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

2. 2

   Объем цилиндра V = hπr2, где V — объем, h — высота, r — радиус цилиндра. Цилиндр — геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными круглыми плоскостями.
   X
   Источник информации

   Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

3. 3

   Объем конуса V = (1/3)hπr2, где V — объем, h — высота, r — радиус конуса. Конус — тело с круглым основанием и вершиной над ним. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
   X
   Источник информации

4. 4

   Объем шара V = 4/3πr3, где V — объем, r — радиус шара. Шар — абсолютно круглое тело.
   X
   Источник информации

   Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

• Если вы не уверены в правильности ваших вычислений, проверьте ответ, воспользовавшись калькулятором или помощью другого человека, разбирающегося в математике.
• Кубические сантиметры — единица измерения объема, то есть количественной характеристики пространства, занимаемого телом.
• Для точного измерения величин используйте линейку или рулетку (особенно если вы делаете важные измерения).

Как высчитать куб бетона для ленточной базы

Калькулятор ленточного фундамента

Основание ленточного типа достаточно популярно. Оно используется для строительства частных домов, хозяйственных построек и дачных строений. Конструкция представляет собой цельную ленту из бетона, армированную стальными прутками. Монолитная лента повторяет контур строения, включая внутренние перегородки.

Таблица состава и пропорций бетонной смеси

Расчет объема бетона для монолитного ленточного фундамента производится по простой формуле V = AхBхP. Расшифруем ее:

• V – потребность в бетонном растворе, выраженная в кубических метрах;
• A – толщина фундаментной ленты;
• B – высота ленточные базы, включая подземную часть;
• P – периметр формируемого ленточного контура.

Перемножив между собой данные параметры, вычислим суммарную кубатуру бетонного раствора.

Рассмотрим алгоритм вычислений для ленточного основания с размерами 6х8 м, толщиной 0,5 м и высотой 1,2 м. Выполняйте расчет по следующему алгоритму:

1. Рассчитайте периметр, удвоив длину сторон 2х(6+8)=28 м.
2. Вычислите площадь сечения, перемножив толщину и высоту ленты 0,5х1,2=0,6 м2.
3. Определите объем, перемножив периметр на площадь сечения 28х0,6=16,8 м3.

Схема ленточного фундамента

О площади здания и составляющих элементах дома

Общую площадь дома можно определить поэтажным суммированием площадей помещений, измеряя их длину и ширину, замерам подлежат чердачные помещения и переходы между зданиями, балконы и лоджии, террасы и веранды. Согласно СНиП, замеры производят на уровне напольного покрытия, плинтусы не учитывают – считают от стенового покрытия. В пределах одного этажа учитывают атриумы – центральные помещения в многоэтажных домах, освещаемые через купольный фонарь или проём в перекрытии, и лифтовые шахты.

Чердачные помещения измеряют по их стенам, отбрасывая незадействованные пазухи чердака. Не учитываются в общей площади дома:

• подвалы с потолком ниже 180 сантиметров, в том числе технического назначения;
• при той же высоте неиспользуемые чердачные и межэтажные коммуникационные помещения;
• лестницы без навеса, наклонные съезды с крыльца – пандусы, расположенные вне здания.

По СНиП, если у мансардных помещений стенами служат скаты крыши, результаты измерений поправляются на коэффициент 0,7. Замеры производятся на высоте от пола 150 см при уклоне стен 30 градусов, 110 см при 45 и 50 см, если уклон круче 60 градусов.

Помимо, поэтажных площадей дома замеряют также и площадь его застройки – это поверхность земли, уровень цокольного этажа, включая все выступы по внешнему периметру, проезды сквозь здание и под столбчатыми опорами также включаются в расчет.

14 Способы перевода кубометров в другие кубические единицы

Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.

Если V измерен в мм3, см3, дм3, л, то в м3 переводим соответственно:

• 1 м3 = 1 мм3 х х 0, 000000001 = 1 мм3 х 10-9;
• 1 м3 = 1 см3 х 0, 000001 = 1 см3 х 10-6;
• 1 м3 = 1 дм3 х 0,001 = 1 дм3 х 10-3. Такой же перевод применяют и для литров, поскольку в 1 л содержится 1 дм3.

Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м3), получим V материала (м3).

Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.

Источники

• https://ru.onlinemschool.com/math/formula/volume/
• https://exceltut.ru/formuly-obema-geometricheskih-figur-najti-vse-obemy/
• https://zametkiddach.ru/obem-bochki-kalkulyator
• https://iobogrev.ru/rasschitat-obem-baka-v-litrah-po-razmeram
• https://StroySoveti.ru/kanalizaciya/kak-rasschitat-obem-emkosti-razlichnoy-formyi.html
• https://VseProTruby.ru/vodoprovodnye/raschet-obema-vody-v-trube.html
• http://LediZnaet.ru/deti/mir-znanij/kak-poschitat-obyom.html

Шаги

Метод 1 из 1:

Нахождение объема цилиндра

1. 1

   Найдите радиус основания. Оба основания равны. Если радиус дан, перейдите к следующему шагу. В противном случае измерьте круг в его самой широкой части, чтобы найти диаметр. Диаметр разделите на 2 и получите радиус. Например, радиус цилиндра равен 1 см.

   • Если дан диаметр, разделите его на 2 и получите радиус.
   • Если дана длина окружности, разделите ее на 2π и получите радиус.

2. 2

   Найдите площадь основания по формуле: A = πr2. Просто подставьте в нее радиус. Вот как это делается:

   • A = π x 12 =
   • A = π x 1.
   • Так как π ≈ 3,14, то площадь основания равна 3,14 см2.

3. 3

   Найдите высоту цилиндра. Если она дана, перейдите к следующему шагу. В противном случае измерьте ее линейкой. Высота – это расстояние между двумя основаниями. Например, высота равна 4 см.

4. 4

   Умножьте площадь основания на высоту, чтобы найти объем цилиндра. Площадь основания равна 3,14 см2, а высота – 4 см, поэтому 3,14 см2 x 4 см = 12,56 см3

   Объем измеряется в кубических единицах, так как это величина, характеризующая объемные (трехмерные) фигуры.

• Придумайте несколько задач и попрактикуйтесь.
• Измеряйте все точно.
• Проще воспользоваться калькулятором.
• Помните: диаметр – наибольшее расстояние между двумя точками на окружности. Так что прижмите точку начала отсчета линейки к краю цилиндра и найдите самое большое расстояние до другого края. Это и будет диаметр.
• В общих случаях объем всегда равен произведению площади основания фигуры на ее высоту (это не работает в некоторых случаях, например, в конусе).
• Для получения радиуса проще найти диаметр и разделить его на два.
• Объем цилиндра вычисляется по формуле: V = πr2h.
• Перемножение площади основания и его высоты аналогично сложению множества его оснований (представьте прозрачный цилиндр, наполненный его основаниями).

Площадь пола или потолка

Потолка и пол в обычной квартире одинаковые. Как посчитать квадратные метры? Очень просто. Если помещение мансардное, тогда потолка там нет – есть только пол и стены. Этап № 1. Измерить длину комнаты и записать полученное число на бумаге. Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).

Этап № 2. Измерить ширину комнаты и записать аналогично. К примеру – 3м.

Этап № 3. Теперь необходимо перемножить эти два числа. Пример: 5 x 3 = 15м. Итак, площадь пола – 15 кв. м. Следовательно, размер потолка также будет равняться 15 кв. м. Записать это число отдельно и обвести ручкой.

Строительный объём

Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.

Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.

L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.

Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.

Если известна общая площадь, можно использовать формулу:

В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.

Если известна площадь застройки

Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:

S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.

S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.

Решение задач на количество вещества, массу и объем

Ключевые слова: решение задач на количество вещества, решение задач по химии на массу и объем, какое количества вещества содержится, какое число молекул содержится, определите объем (н.у.), определите массу, какова масса порции, определите молярную массу, назовите вещество, найдите молярную массу, определите абсолютную массу молекулы, сколько атомов содержится, определите относительную плотность.

ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Количество вещества характеризует число структурных единиц (атомов, молекул, ионов), которое содержится в определенном образце данного вещества. Единицей измерения количества вещества является моль. Количество вещества (ν) связано с числом структурных единиц (N) в образце вещества, его массой (m) и объемом (V) — для газообразных веществ при н. у. — следующими уравнениями:

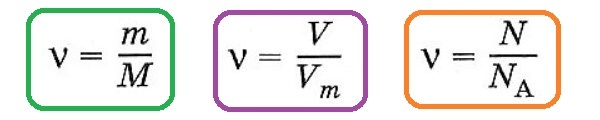в которых

Vm = 22,4 л/моль (мл/ммоль, м3/кмоль) при н.у.,Na = 6,02 • 1023 (постоянная Авогадро),
а молярная масса (М) численно равна относительной молекулярной массе вещества:

Наличие подобной взаимосвязи позволяет, зная одну из величин (количество вещества, массу, объем, число структурных величин) определить все другие величины.

РЕШЕНИЯ ПРОСТЫХ ЗАДАЧ

Задача № 1.
 Какое количество вещества содержится в 33 г оксида углерода (IV)?

Ответ: ν(СО₂) = 0,75 моль.

Задача № 2.Какое число молекул содержится в 2,5 моль кислорода?

Ответ: N(O₂) = 1,505 • 1024.

Внимание! В данном конспекте рассматриваются задачи обычной сложности. Решение сложных задач и задачи с кратким ответом смотрите в конспекте «Решение задач на количественные характеристики«

Задача № 3.Определите объем (н. у.), который займут 0,25 моль водорода.

Задача № 4.Какую массу будет иметь порция оксида серы (IV), объем которой 13,44 л (н. у.)?

Задача № 5.Имеется 3 моль кислорода О₂ при н.у. Определите массу кислорода, его объем, а также число имеющихся молекул кислорода.

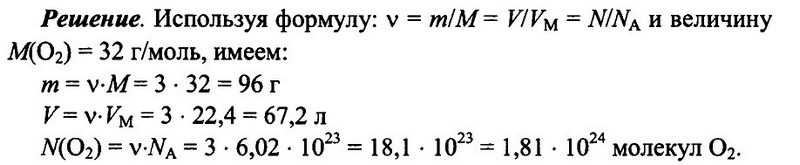
Ответ: m = 96 г; V = 67.2 л;  N(O₂) = 1,81 • 1024.

Задача № 6.Имеется 10 г водорода Н₂. Определите количество водорода, его объем при н.у., а также число имеющихся молекул водорода.  

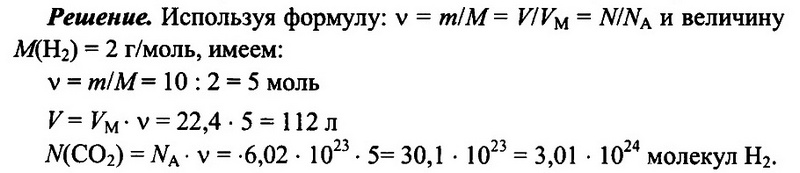
Ответ:  5 моль;   112 л;   3,01 • 1024.

Задача № 7.Имеется 56 л хлора Сl₂ при н.у. Определите количество вещества хлора, его массу и число имеющихся молекул хлора. 

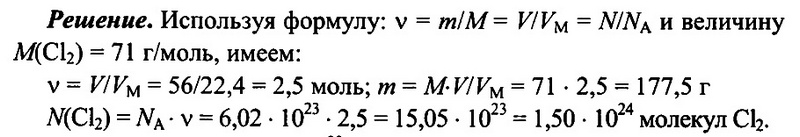
Ответ:  2,5 моль;   177,5 г;   1,5 • 1024.

Задача № 8.Имеется 2,4 • 1023 молекул оксида углерода (IV) СO₂. Определите количество вещества углекислого газа, его массу, а также объем (н.у.) углекислого газа.

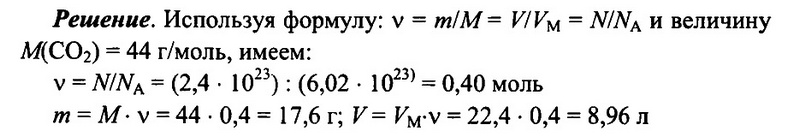
Ответ:  0,4 моль;   17,6 г;   8,96 л.

Задача № 9.Какова масса порции оксида азота (IV), содержащей 4,816 • 1023 молекул? Каков ее объем (н. у.)?

Задача № 10.Масса порции простого вещества, содержащей 1,806 • 1024 молекул, равна 6 г. Определите молярную массу данного вещества и назовите его.

Внимание! В данном конспекте рассматриваются задачи обычной сложности. Чтобы перейти к конспекту решения сложных задач на количественные характеристики и задачи с кратким ответом нажмите на кнопку ниже…. Решение задач на количество вещества, массу и объем

Выберите дальнейшие действия:

Решение задач на количество вещества, массу и объем. Выберите дальнейшие действия:

• Перейти дальше: Решение задач с долей вещества в смеси, в соединении
• Вернуться к списку конспектов по Химии.
• Проверить знания по Химии.

12 Как вычислить объём цистерны выполненной в виде цилиндра

Подобные геометрические фигуры используются для хранения пищевых продуктов, транспортирования топлива и других целей. Многие не знают, как рассчитать объем воды, но основные нюансы такого процесса опишем дальше в нашей статье.

Высоту жидкости в цилиндрической ёмкости определяют по специальному устройству метрштоку. В данном случае емкость цистерны вычисляется по специальным таблицам. Изделия со специальными таблицами измерения объёма в жизни встречаются редко, поэтому подойдём к решению проблемы другим путём и опишем, как рассчитать объём цилиндра по специальной формуле – V=S*L, где

• V- объём геометрического тела;
• S – площадь сечения изделия в конкретных единицах измерения (м³);
• L – длина цистерны.

Показатель L можно измерить при помощи всё той же рулетки, но площадь сечения цилиндра придётся считать. Показатель S вычисляют по формуле S=3,14*d*d/4, где d – диаметр окружности цилиндра.

А теперь ознакомимся с конкретным примером. Допустим, длина нашей цистерны имеет значение 5 метров, её диаметр 2,8 метра. Сначала вычислим площадь сечения геометрической фигуры S= 3,14*2,8*2,8/4=6,15м. А теперь можно приступать к вычислению объёма цистерны 6,15*5= 30,75 м³.

12.1 Как рассчитать объем цилиндра с помощью калькулятора

Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:

1. площадь основания и высота цилиндра;
2. радиус основания и высота цилиндра;
3. диаметр основания и высота цилиндра.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.

Можно ли рассчитать степень, измерив компрессию?

Компрессия напрямую зависит не только от понятия степени сжатия двигателя, но и от природы сжимаемого газа и условий в камере сгорания. На практике зависимость этих параметров выливается в формулу Р = Ро*Ɛƴ, где

• Ро – начальное давление в цилиндре, принимаемое за 1;
• Ƴ – адиабатический показатель для воздуха. В двигателе внутреннего сгорания при сжатии часть тепла отдается стенкам цилиндра, камеры сгорания; происходит утечка части газа через неплотности, а воздух перемешан с частичками топлива, поэтому процесс считается недиабетическим. Показатель политропы при этом равняется не эталонным 1.4, а приближенным к фактическим 1.2.

Все это значит, что, измерив компрессию, мы можем вычислить показатель степени сжатия двигателя. К примеру, при компрессии 15,8 степень сжатия будет близка к 10 единицам. Чтобы уменьшить погрешность, нужно соблюсти все правила измерения компрессии:

1. Свечи должны быть выкручены.
2. Дроссель открыт на 100%.
3. Отключена подача топлива.
4. АКБ должна быть полностью заряжена. При этом емкости должно хватать на измерения компрессии во всех котлах.
5. Стартер должен быть исправен, а на проводах его питания отсутствует значительное падение напряжение из-за окислов.

Печать

Формула расчёта строительного объёма здания.

Чтобы посчитать строительный объём необходимы основные размеры строения, сооружения. L — длинна здания, L1 — ширина, h — высота по боковой стене, h1 — высота в коньке для здания со скатной кровлей. Данные размеры просто получить из наружных обмеров, например при помощи лазерной рулетки. Самая простая формула предполагает вычисление объёма прямоугольника, где высота умножается на длину и на ширину здания. В расчёте не нужно учитывать высоту парапетов здания, которые поднимаются выше кровли. Формула: L х L1 х h = V. Для более сложных строительных конструкций, которые имеют сложную форму и много геометрических размеров, необходимо условно разбить конструкцию на несколько простых объёмных фигур и вычислив объём каждой по простой формуле сложить полученные результаты. Формула, которая используется для расчёта в нашем калькуляторе: L х L1 х h = V1 — это объём нижней части здания до кровли. (h1-h)/2 х L х L1 = V2 — это объём кровельной части здания, для зданий со скатной кровлей. V1 + V2 = V — полный строительный объём здания для дома с двускатной крышей.