Как найти площадь фигуры

В словаре Д.Н. Ушакова

ПЛО́ЩАДЬ, площади, пред. о площади и (·устар.) на площади, мн. и площадей, ·жен. (·книж. ).1. Часть плоскости, ограниченная ломаной или кривой линией (геом.). Площадь прямоугольника. Площадь криволинейной фигуры.2. только ед. Пространство, поверхность, естественно ограниченная или специально выделенная, отделенная для какой-нибудь цели. Количество эксплоатируемой, полезной площади.| Помещение, обычно измеряемое в квадратных метрах поверхности пола. Жилая площадь. Площадь дома.| Пространство земли, занимаемое чем-нибудь. Площадь посева. Культурная площадь (см. культурный» title=’что такое культурный, значение слова культурный в словаре Ушакова’>культурный). Расширение посевной площади. Лесная площадь.3. Большое, ровное и незаостренное место в пределах города или села. Базарная площадь. Красная площадь в Москве. «Внизу народ на площади кипел.» Пушкин. «Там Минин и Пожарский торжественно стоят на площади.» Некрасов.

Как рассчитать площадь комнаты – пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

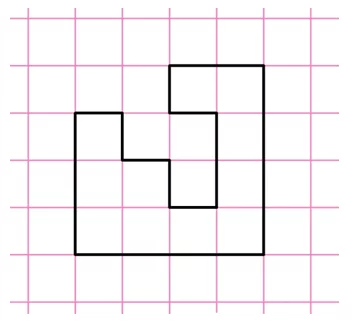
Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

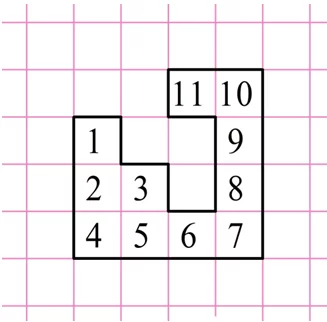
В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

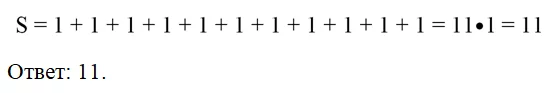
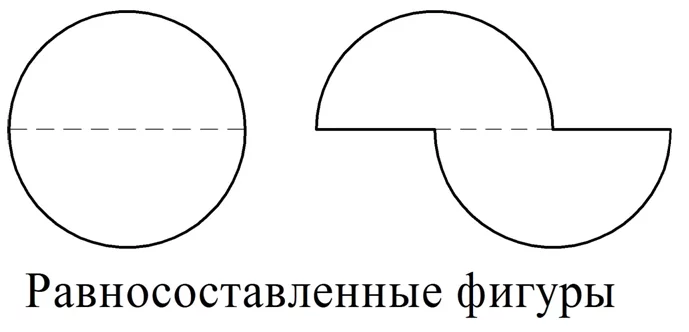
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут

Равносоставленные же фигуры могут и не накладываться друг на друга.

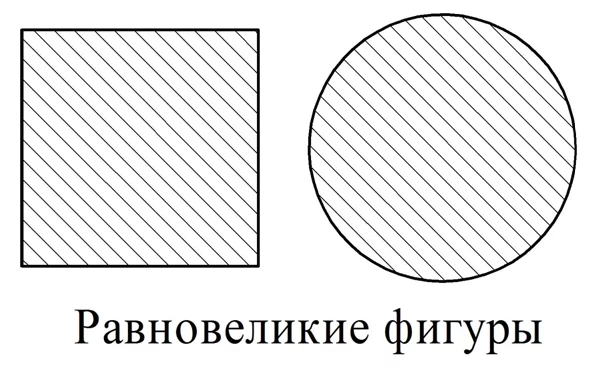
Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны

Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

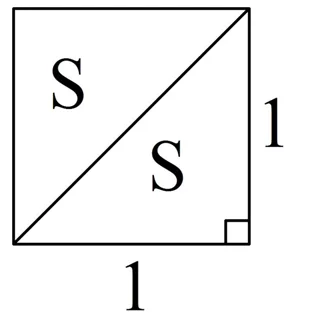
Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

• площадь квадрата со стороной 1 равна единице:
• равносоставленные фигуры имеют равную площадь.

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Формулы для нахождения площадей

•  На завтрак были круглая яичница, параллелепипедная булочка
  и кофе в цилиндрической кружке.
• Геометрия мне очень даже пригодилась в жизни, да.

       В стать «Есть ли у треугольника площадь» мы рассмотрели основные формулы для нахождения площади простейших геометрических фигур. Для решения большинства задач по нахождению площади плоских фигур эти формул вполне достаточно.

Их обычно используют при решении типовых задач на контрольных или при сдаче ЕГЭ. Но вы должны понимать, это далеко не полный список формул для нахождения площади геометрических фигур. Более того, это лишь вершина айсберга.

Взгляните что там, в глубине.

Формулы площади квадрата

      Всем хорошо известны формулы для нахождения площади квадрата с известной стороной или диагональю. Но как быть, если эти величины нам неизвестны? Все очень просто! Нам помогут формулы для нахождения площади квадрата через:

1. радиус вписанной окружности
2. радиус описанной окружности

линию выходящую из угла на
середину стороны квадрата

через периметр

Формулы площади прямоугольника

      Для прямоугольника помимо общеизвестной формулы нахождения площади перемножением длин двух его сторон существуют формулы для нахождения площади через:

известные диагонали и угол между ними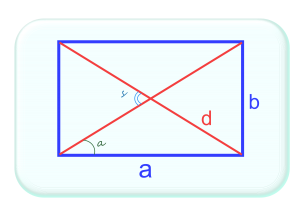

известную длину стороны и угол между этой стороной и диагональю

известный периметр и длину одной стороны

Формулы площади треугольника

•     Все хорошо знают три основные формулы нахождения площади треугольника. Добавлю еще парочку:
• по трем сторонам и радиусу вписанной окружности
• здесь p=(a+b+c) — полупериметр
• по трем сторонам  и радиусу описанной окружности

Формулы площади параллелограмма

1.     Для нахождения площади параллелограмма также существует несколько дополнительных формул:
2. по известным диагоналям и углу между ними
3. по двум известным высотам и углу между ними

Формулы площади четырехугольника

• формула площади выпуклого четырехугольника по известным длинам диагоналей и углу между ними
• формула площади выпуклого четырехугольника по длине периметра и радиусу вписанной окружности
• здесь p= (a+b+c+d)/2 — полупериметр
• формула площади выпуклого четырехугольника по известным длинам сторон и значениям противоположных углов
• здесь p=(a+b+c+d)/2 — полупериметр
• Θ=(f1+f2)/2 — полусумма углов
• формула площади выпуклого четырехугольника вокруг которого можно описать окружность
• здесь p=(a+b+c+d)/2 — полупериметр

      Теперь вы знаете достаточно формул для нахождения площадей плоских фигур. Этого вполне достаточно для того спокойно чувствовать себя на экзамене и чтобы спокойно решать простейшие задачки по ЕГЭ. Но не надо думать, что способы нахождения площади ограничиваются этими формулами.  Ведь помимо уже известных вам треугольников и квадратов существует огромное множество самых разнообразных геометрических фигур, таких как вогнутые четырехугольники, выпуклые и вогнутые многоугольники, а также фигуры , вообще не имеющие какой-либо определенной формы. Кроме того, существуют способы нахождение площади по формулам аналитической геометрии (когда известны координаты вершин или вектора сторон), или с помощью интегрального исчисления.

Ну а в заключение хочу вам представить еще одну универсальную формулу − формулу для нахождения площади эллипса: площадь эллипса равна произведению длин большой и малой полуосей эллипса на число ∏

4 Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

4.1 Как измерять стены с дверью и окном?

Если в комнате есть окно или дверь, то для получения актуальных показателей их необходимо обязательно измерить. Воспользовавшись все той же рулеткой, узнайте высоту и ширину оконного проема, умножьте один результат на другой и вычтите это произведение из общей площади. Не надейтесь на то, что их форма является правильной.

Приведем пару примеров.

Пример 1. Стена с дверным проемом:

• Общая S стены – 2,7 м х 8,0 м = 21,6 м2;
• S дверного проема в стене – 2,3 м х 0,9 м = 2,07 м2;
• S стены без дверей – 21,6 м2 – 2,07 м2 = 19,53 м2.

Пример 2. Стена с оконным проемом:

• Общая S стены – 2,4 м х 5 м = 12 м2;
• Площадь окна – 1,4 м х 1,65 м = 2,24 м2;
• S стены без окна – 12 м2 – 2,24 м2 = 9,76 м2.

4.2 Что нужно, чтобы рассчитать площадь стен?

Рассчитать площадь стен дома можно либо онлайн, либо вручную. Второй вариант более трудоемкий, но точный и подходит в случае, если нет доступа к интернету по тем или иным причинам. Для расчетов потребуется:

• карандаш или ручка;
• листок бумаги;
• калькулятор;
• длинная линейка;
• уровень;
• рулетка.

Важно! Зная точную площадь стен и помещения, можно приобрести нужное количество строительных материалов, необходимых для ремонта. Площадь измеряют квадратными метрами и обозначают м2

На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы. И по мере получения замеров, их наносят на чертеж.

4.3 Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах

4.4 Как посчитать квадратные метры стены с дверью

Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.

Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

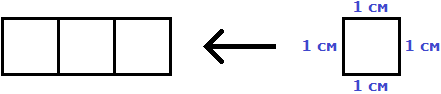
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

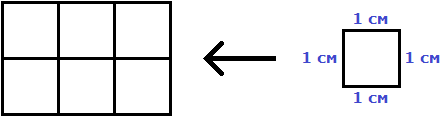
Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Как рассчитать площадь потолков и стен

Пло­щадь потол­ка обыч­но рав­на пло­ща­ди пола, за исклю­че­ни­ем мно­го­уров­не­вых потол­ков, поэто­му отдель­но её вычис­лять не требуется.

S стен необ­хо­ди­ма чаще все­го для опре­де­ле­ния коли­че­ства кера­ми­че­ской плит­ки или руло­нов обоев.

• Если обо­я­ми или плит­кой закры­ва­ет­ся все сте­ны, то про­ще вна­ча­ле рас­счи­тать общий пери­метр поме­ще­ния Р, сло­жив все дли­ны его стен. Р = 2 * (а + b).
• Затем Р нуж­но умно­жить на высо­ту стен h. Полу­ча­ем сум­мар­ную пло­щадь всех стен S.
• Теперь из S стен вычи­та­ет S окон и двер­но­го про­ема, пред­ва­ри­тель­но рас­счи­тан­ных по фор­му­ле (1).

Таким обра­зом S под отдел­ку опре­де­ля­ет­ся по такой фор­му­ле: S отд. = (2 * (а + b) * h) — S окон — S две­рей (6).

Если про­из­во­дит­ся частич­ная отдел­ка, то рас­счи­ты­ва­ет­ся пло­щадь поверх­но­сти сте­ны, пред­на­зна­чен­ной для отделки.

При­мер, как най­ти пло­щадь S отд. для сте­ны с дверью:

S отд. = S сте­ны – S две­ри = 4 * 2.7 – 1 * 2.1 = 8.7 м2.

 Как высчитать, сколько нужно плитки для фартука

• Что­бы выло­жить фар­тук из плит­ки на кухне, нуж­но вна­ча­ле про­из­ве­сти его раз­мет­ку и заме­рить дли­ну и высоту.
• Затем по ф‑ле (1) рас­счи­ты­ва­ем пло­щадь фартука.
• Для рас­че­та коли­че­ства плит­ки необ­хо­ди­мо S фар­ту­ка раз­де­лить на S одной плит­ки: N пл. = S фарт. / S пл. одной плит­ки (7).
• К рас­чёт­но­му коли­че­ству N нуж­но при­ба­вить ещё 5 — 10%, с учё­том нарез­ки угло­вых пли­ток и неиз­беж­но­го части мате­ри­а­ла в рас­ход (часть плит­ки бра­ку­ет­ся плиткорезом).

То есть ито­го­вое коли­че­ство будет рав­но: N итог. = N пл. + N пл. * (0.05 — 0.1) (8).

Коли­че­ство плит­ки для ван­ной, если ею закры­ва­ют­ся все сте­ны, рас­счи­ты­ва­ет­ся по мето­ду, опи­сан­но­му выше:

• по фор­му­ле (6) рас­счи­ты­ва­ем S отде­лоч­ной поверх­но­сти стен.;
• по ф‑лам (7) и (8) — коли­че­ство плитки.

Как посчитать количество обоев

Рас­чёт необ­хо­ди­мо­го коли­че­ства обо­ев более сло­жен, так как необ­хо­ди­мо учитывать:

• шаг узо­ра обоев;
• запас на отрез.

Коли­че­ство руло­нов счи­та­ют дву­мя способами:

• по пло­ща­ди стен;
• по пери­мет­ру поме­ще­ния и коли­че­ству полотен.

Суще­ству­ют гото­вые таб­ли­цы рас­че­тов обоев.

Первый способ расчета

Пер­вый спо­соб про­стой, но он весь­ма при­бли­зи­тель­ный, поэто­му при­хо­дит­ся поку­пать обои с боль­шим запа­сом, что неэкономно.

• Рас­счи­ты­ва­ет­ся пло­щадь поверх­но­сти отдел­ки S отд. за выче­том окон и две­рей — по ф‑ле (6).
• Опре­де­ля­ет­ся пло­щадь одно­го руло­на: дли­на руло­на умно­жа­ет­ся на его шири­ну. Напри­мер, если в рулоне шири­ной 60 см 10 мет­ров полот­на, то S одно­го руло­на будет 6 м2.
• Затем делим S отд. на S одно­го руло­на, и полу­чен­ную циф­ру округ­ля­ем до цело­го числа.
• При­бав­ля­ем один — два руло­на в запас.

Второй способ расчета

Вто­рой спо­соб более точен и эко­но­мен, но и более сложен:

• Высчи­ты­ва­ем пери­метр части поме­ще­ния Р, без окон­ных и двер­ных про­емов, на кото­рые пой­дут целые полотна.
• Опре­де­ля­ем дли­ну одно­го цело­го полот­на l ц.: к высо­те поме­ще­ния (обыч­но 2.60 м) при­бав­ля­ем запас на узор 0.5 м и на отрез — 0.1 м.
• Высчи­ты­ва­ем коли­че­ство целых поло­тен N ц., раз­де­лив Р на l ц.
• Теперь рас­счи­та­ем таки­ми же спо­со­ба­ми дли­ну l к. и коли­че­ство N к. кус­ков поло­тен над окна­ми, две­ря­ми и под окнами.
• Опре­де­ля­ем общий мет­раж целых поло­тен L ц. = N ц. * l ц.
• Высчи­ты­ва­ем, сколь­ко все­го мет­ров будет выре­зан­ных кус­ков L к. = N к. * l к.
• Рас­счи­ты­ва­ем общую дли­ну поло­тен: L общ. = L ц. + L к.

Теперь необ­хо­ди­мо посчи­тать сколь­ко все­го руло­нов нуж­но. Для это поде­лим L общ. на дли­ну одно­го руло­на, а полу­чен­ную циф­ру округ­лим в сто­ро­ну увеличения.

При срав­не­нии обе­их спо­со­бов рас­че­та обыч­но наблю­да­ет­ся раз­ни­ца в один рулон. Если не хочет­ся мучить­ся со вто­рым мето­дом, мож­но посту­пить про­ще: опре­де­лить коли­че­ство руло­нов по пер­во­му спо­со­бу и доба­вить про запас не два руло­на, а один.

Про­из­ве­дя рас­чет обо­ев, мож­но срав­нить теперь полу­чен­ную циф­ру с табличной.

Таким обра­зом реше­ние про­стой зада­чи как посчи­тать пло­щадь поме­ще­ния пред­став­ля­ет не толь­ко прак­ти­че­ский инте­рес, но и явля­ет­ся непло­хой тре­ни­ров­кой для моз­га. Само­сто­я­тель­ный рас­чет коли­че­ства отде­лоч­но­го мате­ри­а­ла поз­во­ля­ет не допу­стить его перерасход.

1 Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

1.1 Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

1.2 Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

a =

b =

1.3 Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Варианты обозначения

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.

В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.

В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение .

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.

Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.

Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.