Самое большое число
Содержание:
- Идут дольше, но платить меньше
- Использование названий больших чисел
- О бонусах
- Появление названий чисел: какие способы используются?
- Внесистемные числа
- О колониальных войнах и русской душе
- Семья гугол
- О системе
- Тиражные лотереи
- Американская система
- Самое большое число в мире — это число Грэма
- Можно ли выиграть в лотерею и что для этого следует знать
- Самое большое число
Идут дольше, но платить меньше
К тому же, в отличие от карточных, переводы по реквизитам идут дольше. Сначала банк отправляет поручение в Центробанк, а после оно передаётся банку-получателю. Это занимает от трёх до пяти рабочих дней. Карточные переводы шустрее, потому что по договорённости с платёжной системой деньги зачисляются получателю сразу, хотя поступают намного позже.
Тем не менее, у переводов по реквизитам есть ещё одно преимущество — они дешевле, чем карточные. Это связано с тем, что в переводах по картам присутствует ещё один участник (платёжная система), услуги которого нужно оплачивать.
Переводы по реквизитам дешевле. Фото: nb-ugra.ru
Как это выглядит на практике: представим, что нужно перевести 300 тысяч, 700 тысяч, 1 млн, 2 млн и 5 млн рублей. С переводом первой суммы не возникнет больших проблем. Её можно перевести как по реквизитам, так и по номеру карты. Но могут заблокировать, если ранее такие суммы не переводились. 700 тысяч рублей также можно перевести удалённо в любом банке. Но она подпадёт под проверку. Поэтому могут потребовать доказать причины перевода. Суммы свыше 1 млн и 2 млн рублей можно отправить далеко не в каждом банке. Их также будут проверять. 5 млн рублей можно перевести дистанционно, только являясь клиентом «Тинькофф Банка». В других банках лимит на переводы по реквизитам гораздо меньше.
Подводя итог, можно сказать, что переводы по реквизитам позволят сэкономить и обойти лимиты по суммам, но деньги придут не сразу, а операцию всё равно проверят и с большой долей вероятности потребуют дополнительные документы. Карточные переводы быстрые, дорогие и ограниченные. Поэтому использовать их в крупных сделках не имеет смысла.
Использование названий больших чисел
Некоторые имена с большими числами, такие как миллион , миллиард и триллион , имеют реальные ссылки в человеческом опыте и встречаются во многих контекстах. Иногда названия больших чисел были вынуждены широко использоваться в результате гиперинфляции . Банкнота с самой высокой числовой стоимостью, когда-либо напечатанная, была купюрой в 1 секстиллион пенго (10 21 или 1 миллиард билпенго в напечатанном виде), напечатанной в Венгрии в 1946 году. В 2009 году Зимбабве напечатала зимбабвийскую купюру в 100 триллионов (10 14 ) долларов , которая в то время печати стоило около 30 долларов США.
Однако имена больших чисел имеют незначительное, искусственное существование, редко встречаются вне определений, списков и обсуждений способов именования больших чисел. Даже хорошо зарекомендовавшие себя названия, такие как секстиллион , используются редко, поскольку в контексте науки, включая астрономию, где часто встречаются такие большие числа, они почти всегда записываются с использованием научных обозначений . В этих обозначениях степени десяти выражаются как 10 с числовым надстрочным индексом, например: «Рентгеновское излучение радиогалактики равно1,3 × 10 45 джоулей » . Когда такое число, как 10 45, нужно передать словами, оно просто читается как« от десяти до сорок пятого ». Это легче сказать и менее двусмысленно, чем« quattuordecillion », что означает нечто иное в длинном и коротком масштабе.
Когда число представляет собой количество, а не количество, можно использовать префиксы SI — таким образом, «фемтосекунду», а не «одну квадриллионную долю секунды» — хотя часто вместо некоторых очень высоких и очень низких префиксов используются степени десяти. В некоторых случаях используются специальные единицы, такие как парсек астронома и световой год или сарай физика элементарных частиц .
Тем не менее, большие числа обладают интеллектуальным увлечением и представляют математический интерес, и присвоение им имен — один из способов, с помощью которых люди пытаются осмыслить и понять их.
Одним из самых ранних примеров этого является «Счетчик песка» , в котором Архимед дал систему именования больших чисел. Для этого он называл числа до бесчисленного множества (10 8 ) «первыми числами» и называл 10 8 «единицей вторых чисел». Кратные этой единицы затем стали вторыми числами, до этой единицы взято мириады раз, 10 8 · 10 8 = 10 16 . Это стало «единицей третьих чисел», кратными третьим числам и так далее. Архимед продолжал называть числа таким образом до бесчисленного множества раз больше единицы из 10 8-го числа, то есть и встроил эту конструкцию в другую свою копию, чтобы произвести имена для чисел вплоть до Архимеда, а затем оценил количество песчинок, которые потребовалось, чтобы заполнить известную вселенную, и обнаружил, что это не более «тысячи мириад восьмых чисел» (10 63 ).
(108)(108)знак равно108⋅108,{\ displaystyle (10 ^ {8}) ^ {(10 ^ {8})} = 10 ^ {8 \ cdot 10 ^ {8}},}((108)(108))(108)знак равно108⋅1016.{\ displaystyle ((10 ^ {8}) ^ {(10 ^ {8})}) ^ {(10 ^ {8})} = 10 ^ {8 \ cdot 10 ^ {16}}.}
С тех пор многие другие занимались концептуализацией и именованием чисел, которые на самом деле не существуют вне воображения. Одна из причин для такого поиска — это то, что приписывается изобретателю слова гугол , который был уверен, что любое конечное число «должно иметь имя». Другая возможная мотивация — это соревнование между студентами курсов компьютерного программирования, где обычным упражнением является написание программы для вывода чисел в форме английских слов.
Большинство названий, предлагаемых для больших чисел, относятся к систематическим схемам, которые можно расширять. Таким образом, многие имена для больших чисел являются просто результатом следования системе именования до ее логического завершения или дальнейшего ее расширения.
О бонусах
Может возникнуть логический вопрос: а что заставляет ученых работать в этом направлении? Так, это, конечно же, азарт и желание быть первооткрывателем. Однако и тут есть свои бонусы: за свое детище Кертис Купер получил денежный приз в размере 3 тысячи долларов. Но и это еще не все. Специальный Фонд Электронных Рубежей (аббревиатура: EFF) поощряет такие вот поиски и обещает незамедлительно наградить денежным призом в размере 150 и 250 тысяч долларов тех, кто предоставит на рассмотрение простые числа, состоящие из 100 миллионов и миллиарда чисел. Так можно не сомневаться, что в этом направлении сегодня работает огромное количество ученых по всему миру.
Появление названий чисел: какие способы используются?
На сегодняшний день есть 2 системы, согласно которым числам даются наименования, – американская и английская. Первая является довольно простой, а вторая – наиболее распространенной по всему миру. Американская позволяет давать имена большим числам так: вначале указывается порядковое числительное на латинском, а потом идет добавление суффикса «иллион» (исключением здесь служит миллион, означающий тысячу). Такую систему применяют американцы, французы, канадцы, а также используется она и в нашей стране.

Английская широко применяется в Англии и Испании. По ней числа именуются так: числительное на латинском «плюсуется» с суффиксом «иллион», а к последующему (большему в тысячу раз) числу «плюсуется» «иллиард». Например, сначала идет триллион, за ним «шагает» триллиард, за квадриллионом же идет квадриллиард и т.д.
Так, одно и то же число в различных системах может означать разное, к примеру, американский биллион в английской системе именуется миллиардом.
Внесистемные числа
Помимо чисел, которые записываются по известным системам (приведенным выше), существуют еще и внесистемные. Они обладают своими названиями, в которых не включаются латинские префиксы.
Начать их рассмотрение можно с числа, называемого мириадой. Определяется оно как сотня сотен (10000). Но по своему назначению это слово не применяется, а употребляется в качестве указания на бесчисленное множество. Даже словарь Даля любезно предоставит определение такого числа.
Следующим после мириады идет гугол, обозначающий 10 в степени 100. Впервые это наименование было употреблено в 1938 году – математиком из Америки Э.Каснером, отметившим, что это название придумал его племянник.

В честь гугола свое название получил Google (поисковая система). Затем 1-ца с гуголом нулей (1010100) представляет собой гуголплекс – такое название придумал тоже Каснер.
Еще большим по сравнению с гуголплексом является число Скьюза (е в степени е в степени е79), предложенное Скьюзом при доказательстве гипотезы Риммана о простых числах (1933 год). Есть и еще одно число Скьюза, но оно применяется, когда несправедлива гипотеза Риммана. Какое из них больше, сказать довольно сложно, особенно если речь заходит о больших степенях. Однако и это число, несмотря на свою «огромность», не может считаться самым-самым из всех тех, которые обладают своими названиями.
А лидером среди самых больших чисел в мире является число Грэма (G64). Именно его использовали в первый раз для проведения доказательств в области математической науки (1977 год).
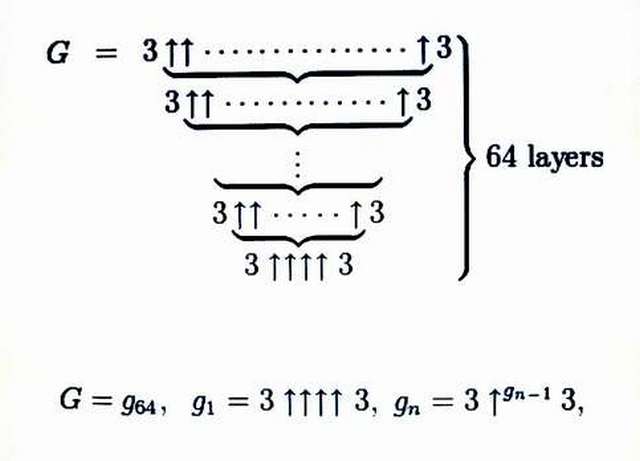
Когда речь идет о таком числе, то нужно знать, что без специальной 64-уровневой системы, созданной Кнутом, не обойтись – причина тому связь числа G с бихроматическими гиперкубами. Кнутом была придумана сверхстепень, а для того чтобы было удобно делать ее записи, он предложил использование стрелок вверх. Вот мы и узнали, как называется самое большое число в мире. Стоит отметить, что это число G попало на страницы известной Книги рекордов.
О колониальных войнах и русской душе
Заводя разговор о самом большом числе, не обойтись без возвращения к основам, чтобы упростить понимание, ведь большинство людей после окончания института или училища вряд ли пользовались вычислениями сложнее уровня «3 ящика на 7 человек».
В мире используют два способа наименования чисел — английский и американский. Первый получил большее распространение — в первую очередь потому, что бывшие колонии наследовали привычные принципы. Названия чисел тут образуются путем добавления к латинскому числительному (tres, quattuor, quinque и т. д.) суффикса «-иллион», а к следующему, большему в 1000 раз, — суффикса «-иллиард». Получается чередование: триллион-триллиард, квинтиллион-квинтиллиард. Выбивается из этого правила только первое число: «миллион» происходит от латинского «тысяча» с добавлением соответствующего суффикса — буквально «тысяча тысяч».
В американском способе именования, который распространен в Канаде, Франции и США, суффикс «-иллиард» не используется вовсе, а латинские числительные просто идут по возрастанию. Так получается, что английский «триллиард» равен американскому «квадриллиону», а вместо миллиардеров в США — биллионеры.
В России заимствовать не стеснялись — хотя считается, что в ходу тут американская система, по факту используют смесь: вместо «биллиона» стабильно вставляют в речь «миллиард», да и «триллиарды» периодически «всплывают».
Семья гугол
Имена гугол и гуголплекс были изобретены племянником Эдварда Каснера Милтоном Сироттой и введены в книгу Каснера и Ньюмана 1940 года « Математика и воображение»
в следующем отрывке:
| Значение | Имя | Власть |
|---|---|---|
| 10 100 | Гугол | Каснер и Ньюман, словари (см. Выше) |
| 10 гугол = 10 10 100 | Гуголплекс | Каснер и Ньюман, словари (см. Выше) |
Конвей и Ричард К. Гай
предположили , что N-Plex можно использовать в качестве имени 10 N . Это дает начало названию гуголплекс за 10 гуголплекс = 10 10 10 100 . Это число (десять в степени гуголплекса) также известно как гуголдуплекс и гуголплекс. Conway и Гай предложили N-MINEX можно использовать в качестве имени для 10 -N , порождая название googolminex для обратной части в гуголплекс. Ни одно из этих имен не широко используется и в настоящее время не встречается в словарях.
Имена гугол и гуголплекс вдохновил название интернет — компании и ее корпоративные штаб — квартиры , то Googleplex , соответственно.
О системе
Как это все происходит, как ученые находят самые большие числа? Так, сегодня большинство работы за них делает компьютер. В данном же случае Купер использовал распределенные вычисления. Что это значит? Эти расчеты ведут программы, установленные на компьютерах пользователей Интернета, которые добровольно решили принять участие в исследовании. В рамках данного проекта было определено 14 чисел Мерсенна, названных так в честь французского математика (это простые числа, которые делятся только сами на себя и на единицу). В виде формулы это выглядит следующим образом: M n = 2 n — 1 («n» в данной формуле — это натуральное число).
Тиражные лотереи
Тиражные лотереи отличаются тем, что призовой фонд разыгрывается между участниками в определенный момент после того, как продажа билетов прекращается. Каждый тираж – это определение выигрышных номеров с помощью соответствующего оборудования.
С онлайн-тиражами каждые 15 минут
Таких лотерей у «Столото» 6. Столько лотерей было создано, чтобы желающий сыграть не дожидался несколько дней каждого тиража. В целом тиражи проводятся каждые 2,5 минуты, что делает эти лотереи «почти моментальными».
Все тиражи проводятся через компьютерную программу – генератор случайных чисел. В алгоритмы заложена частота выигрыша, но какое число выпадет в каждом конкретном случае, программа выбирает случайно.
В каждой из лотерей игрок выбирает несколько чисел из предложенного набора, или по несколько чисел в нескольких полях. Все это непосредственно влияет на вероятность выиграть.
Лотереи такие:
- «Джокер» (нужно угадать 9 чисел из 52 при том, что в тираж отбирается 15 чисел);
- «Рапидо» (нужно угадать 8 цифр из 20 в одном поле и 1 цифру из 4 – в другом поле);
- «12/24» (нужно угадать 12 или 0 чисел из 24);
- «Дуэль» (нужно угадать 2 числа из 26 в одном поле и столько же – во втором);
- «Топ-3» (8 разных вариантов игры, 2 тура)
- «КЕНО-Спортлото» (совпадение 9 цифр билета из 9, или нужно угадать 10 чисел из 80, всего 42 категории выигрышей).
В каждой игре есть свои правила, но мы рассмотрим только вероятность выиграть суперприз – то есть, максимально возможную сумму выигрыша. Так как математически вероятность выиграть будет иметь слишком много знаков после запятой, посчитаем, на сколько билетов приходится 1 суперприз:
| Лотерея | Максимальный выигрыш | Шансы на выигрыш |
|---|---|---|
| «Джокер» | от 200 000 рублей | 1:735 080 |
| «Рапидо» | от 200 000 рублей | 1:503 880 |
| «12/24» | от 500 000 рублей | 1: 2 704 156 |
| «Дуэль» | от 100 000 рублей | 1:105 625 |
| «Топ-3» | до 30 000 рублей | до 1:1 000 |
| «КЕНО-Спортлото» | от 10 000 000 рублей | 1:1 000 000 000 |
Это только максимальные выигрыши, а в каждой лотерее часть призового фонда идет тем, кто угадал часть из всей комбинации.
Также в каждой игре есть дополнительные возможности – умножающие коэффициенты, возможность сыграть несколько тиражей подряд и другие. За это придется доплачивать, но и шансы на выигрыш повышаются.
С «обычными» тиражами
Таких лотерей у «Столото» тоже немало – больше 10. По некоторым тираж проводится 6 раз в день, по некоторым – раз в неделю.
Среди самых известных лотерей – «Русское лото» (проводится с 1994 года), «6 из 36» и «Жилищная лотерея». Все они проводят розыгрыши раз в неделю и транслируют их на канале НТВ.
Другие лотереи («Гослото «4 из 20», «Гослото «5 из 36», «Гослото «7 из 49», «Гослото «6 из 45» и другие) проводят розыгрыш с «реальным» лототроном чаще – от 1 до 6 раз каждый день.
Все лотереи отличаются как своими условиями, так и шансами на выигрыш:
| Лотерея | Что нужно сделать | Выигрыш | Шансы выиграть | Цена билета |
|---|---|---|---|---|
| «Русское лото» | За первые 15 ходов зачеркнуть 15 чисел одного поля | Миллионы рублей, автомобили, дома и т.д. | 1:45 795 673 964 460 800 | 100 рублей |
| «6 из 36» | Угадать все 6 чисел из 36 | От 3 000 000 рублей | 1:1 947 792 | 100 рублей |
| «Жилищная лотерея» | За первые 10 ходов зачеркнуть все 10 чисел любых 2 строчек | Квартира в Москве или 33 000 000 рублей | 1: 381 376 365 460 | 100 рублей |
| «Гослото «4 из 20» | Угадать по 4 цифры из 20 в двух полях сразу | От 50 000 000 рублей | 1:23 474 025 | 200 рублей |
| «Гослото «5 из 36» | Угадать 5 цифр из 36 в одном поле и 1 из 4 – во втором | От 1 000 000 рублей | 1:1 507 968 | 40 рублей |
| «Гослото «7 из 49» | Угадать все 7 чисел из 49 | От 30 000 000 рублей | 1:85 900 584 | 50 рублей |
| «Гослото «6 из 45» | Угадать все 6 чисел из 45 | От 10 000 000 рублей | 1:8 145 060 | 100 рублей |
Отметим, что несмотря на крайне низкую вероятность выиграть джекпот в «Русском лото» или «Жилищной лотерее», случаи крупных выигрышей были. Это связано с тем, что билетов на эти лотереи продается очень много.
Американская система
Интересным окажется тот факт, что данная система используется не только в Америке и Канаде, но и в России. К тому же она имеет и свое научное название: система именования чисел с короткой шкалой. Как же называются в данной системе большие числа? Так, секрет довольно-таки простой. В самом начале будет идти латинское порядковое числительное, после же просто добавится всем известный суффикс «-иллион». Интересным окажется следующий факт: в переводе с латинского языка число «миллион» можно перевести как «тысячища». Американской системе принадлежат следующие числа: триллион — это 10 12 , квинтиллион — 10 18 , октиллион — 10 27 и т. д. Несложно будет также разобраться, сколько же нулей записано в числе. Для этого нужно знать простую формулу: 3*х + 3 (где «х» в формуле — это латинское числительное).
Самое большое число в мире — это число Грэма
Миллион, миллиард (или биллион?), триллион. С каждым разом представлять такие числа все труднее. Чего уж говорить про гугол (единица с сотней нулей) и невообразимый гуголплекс.
А почему бы не пойти дальше и не возвести гуголплекс в степень гуголплекс? Звучит абсурдно и бессмысленно. Однако есть число, которое является не только единицей с большим количеством нулей. У него также есть практическая сторона. Встречайте: число Грэма!
Представьте себе куб, все вершины которого соединены линиями–отрезками двух цветов, красного или синего. Соединены и раскрашены в случайном порядке. Необходимо было подобрать такой комбинацию синих и красных ребер фигуры, чтобы при этом не было четырех вершин одного цвета в одной плоскости.
Задача вполне себе разрешима, но из-за простоты ученые её стали усложнять. Любят же они себя испытывать!
Сначала из куба сделали тессеракт — куб с четырьмя измерениями! Но даже так решение быстро нашли. Затем попробовали с пятью, шестью а затем с семью измерениями. Тут-то и возникла проблема при подсчетах.
Грэм не сумел математически доказать возможность выполнения условий задачи в семимерном, восьмимерном, девятимерном кубе. Однако было недостаточно сказать «я не могу!», чтобы потом всему миру заявить: «это невозможно!». Нужно еще это математически как-то доказать.
Таким образом, Рональд Грэм стал искать нижнюю и верхнюю планку, при которой любая подобная задача на комбинаторику становится неразрешимой. Он определил, что минимальная размерность будет находиться в числе точно больше шести и точно меньше того самого числа, названного в его честь.
Теперь мы подошли к самому главному: как выглядит число Грэма (G)?
А выглядит оно так:
Математик Дональд Эрвин Кнут придумал записывать степень стрелочной нотацией. Вот как выглядит она:
Если в выражении присутствует степень в степени, то она выглядит так:
Стрелочка показывает наличие пирамиды из степеней.
И так каждый раз, пока не дойдем до числа Грэма: G=g64.
По-другому записать его не удастся. Как уже было сказано, банально места не хватит.
Заключение
Математика способна удивлять. Будучи на грани фантастики, она двигает науку вперед, сама создает крышесносные теории и сама же их подтверждает. Ну, как сама. Этим занимаются неординарные персоны, чья сохранившаяся детская наивность позволяет идти на удивительные свершения в области науки. Математика — это не только гигантские числа; это также люди, которые трудятся и изобретают на благо всему обществу.
Полюбить науку с детства очень важно. Математику — еще важнее
Изучая её, изучаешь историю, культуру, физику и другие отрасли научного знания.
В Матклассе продолжают работать онлайн-кружки и курсы по математике для детей от 5 до 99 лет. Также, если ситуация стабилизируется, скоро заработают и занятия в Москве и Калининграде!
Детям нравится изобретать, они получают настоящее удовольствие, когда их логические способности и фантазия оказываются полезными на практике. Так давайте подарим им такой опыт!
Источник
Можно ли выиграть в лотерею и что для этого следует знать
Скептики считают, что в выигрыше остаются исключительно устроители лотерей, оптимисты верят, что «Спортлото», «Гослото» и прочие популярные лотереи – реальный способ обрести настоящее финансовое благополучие.
Сразу скажем, что выиграть в лотерею, конечно, можно, и вероятность взятия джек-пота есть у каждого играющего. Теория вероятности и математика с основами статистики допускают возможность выигрыша любого лотерейного билета в любое время.
Однако в теории игры существует ещё и такое понятие как дистанция, и именно дистанция является главным препятствием на пути рядовых игроков к желанному богатству. Другими словами, с момента ожидания выигрыша и до самого выигрыша может пройти изрядное количество времени. Играть в лотерею можно день, месяц, год, десять лет – и вероятность победы всегда будет примерно одинаковой.
В статье мы постараемся не затрагивать «мистический» аспект игры, но упомянуть о нём всё же следует.
Есть игроки, которые верят в заговоры на удачу, в серии побед, в счастливые дни и номера, в кроличьи лапки и ритуалы. Примерам невероятной удачливости посвящено множество фильмов, книг и телепередач. Однако в реальности всё обстоит более прозаично: играя в лотерею, мы имеем дело с математической теорией игры и не более.
Безусловно, вера в собственные силы и здоровый оптимизм – условия, работающие скорее в плюс, чем в минус. Человек, который верит в удачу, чаще оказывается прав, чем безнадёжный пессимист.
В настоящее время стали очень популярны онлайн лотереи, которые почти не отличаются от привычных нам «бумажных» и оффлайновых лотерей.
О том, как это работает, смотрите небольшое видео:
Крупный выигрыш в России на зарубежной лотерее онлайн
Кстати, не так давно — в феврале 2016 года — мужчина из Подмосковья, С.К., который работает персональным водителем, выиграл с помощью подобной он-лайн лотереи 824 000 евро!
По словам мужчины — победителя лотереи, он играет относительно недавно, всего несколько месяцев. Но это не стало помехой, удача улыбнулась ему и джек-пот лотереи «Австрия-лото» успешно перекочевал к отцу троих детей из России.
По понятным причинам счастливчик решил не показывать своего лица, а мы можем лишь поздравить его и пожелать вам, уважаемые читатели, также оказаться в числе обладателей круглых сумм.
А мы продолжаем… Какие способы выигрыша в лотерею существуют, вы узнаете, дочитав статью до конца.
В своё время было проведено множество научных исследований, посвященных теории игры. Ученых заинтересовал вопрос: есть ли какие-то закономерности, на основе которых можно создать стратегию или систему для увеличения вероятности выигрыша?
Реально ли, например, при теоретически безлимитном количестве средств получать больше, нежели тратить на приобретение билетов?
Результаты исследований оказались весьма неутешительными, но вполне закономерными с точки зрения науки. Их можно изложить в нескольких пунктах:
- Вероятность выпадения любых номеров строго равномерна;
- Не существует способов увеличить вероятность угадывания номеров в сравнении с чисто случайным выбором;
- Абсолютно выигрышных стратегий не существует.
Другими словами, приговор математиков был таков: ставь случайно и жди удачи.
Однако исследования теории игр на этом не прекратились. Точные науки поводов для оптимизма не внушали, поэтому за дело взялись психологи.
Основанием послужил тот факт, что на размер выигрыша влияет не только математика, но и мышление участников лотереи. Чем большее количество людей выберет одинаковую игровую комбинацию, тем меньше денег они получат, если эта комбинация окажется выигрышной.
Таким образом, цель любого игрока – в самой «маленькой компании»: то есть, выбрать такие номера, которые с наименьшей вероятностью выберут другие участники тиража.
Идея сторонников психологической теории заключалась в следующем: играть следует не против лототрона (раз его обыграть нельзя), а против остальных игроков.
Для этого необходимо «всего лишь» изучить психологию типичного участника лотереи и учитывать их при составлении выигрышной комбинации.
Действительно: в том, как участники выбирают (зачеркивают) числа в лотереях, есть определённые закономерности. Задача игрока с научным подходом – избегать стереотипов мышления при выборе «счастливых» номеров.
Самое большое число
Самое большое простое число в мире – 274207281 – 1, которое содержит 22 338 618 десятичных цифр (простое число Мерсенна). Значение нашли в 2015 году в ходе проекта по распределенному поиску простых чисел Мерсенна GIMPS. Поясним, что простыми называются натуральные (целые положительные) числа, имеющие только два делителя — единицу и само себя. Например, 2, 3, 5, 7 — простые числа. Список продолжают 11, 13, 17, 19… Кроме двойки все числа нечетные, иначе бы делились не только на единицу и себя, но и на два. Значит, найденное простое число еще и самое большое из нечетных.
Маренн Марсен и самое большое простое число
По утверждению Евклида, простых чисел бесконечное множество, значит, наибольшего простого числа нет. Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.
Есть специальный способ проверки простоты чисел, который называется тест Люка-Лемера. Правда, предназначен он исключительно для чисел Мерсенна. Что же это за числа? Это вид натуральных чисел, расположенных в определенной последовательности. Имя им дал французский математик Мерсенн Марен. Вид числа Мерсенна такой:
Mn = 2n – 1,
где n — натуральное число.
При n = 1, 2, 3, 4, … числа Мерсенна образуют последовательность, начинающуюся с 1, 3, 7, 15. Затем идут 31, 63, 127. Продолжают ряд 255, 511, 1023, 2047 и т.д.
Такие числа используют в криптографии, например, для усовершенствования банковских кодов.