Быстрый перевод единиц площади земельного участка

Единицы измерения длины в Российской Империи

Во времена Древней Руси для измерения длины были приняты основные меры. 

Впоследствии к ним присовокупили более современные, но старые оставили в употреблении:

1. Малая пядь (она же четверть) — от вытянутого большого до указательного пальца (17-19 см). Существовала и великая пядь — от большого до мизинца (22-23 см).
2. Локоть — расстояние от локтя до кулака, или до конца вытянутых пальцев, что вносило свои коррективы. Считался основной мерой при торговле тканью и равнялся примерно 46 сантиметрам.
3. Разновидностей сажени насчитывалось почти десять (косая, большая, печатная и другие). Простая сажень — примерно 152 см, от кончиков больших пальцев на руках, вытянутых по ширине плеч. Маховая сажень измерялась почти так же, но не по большим пальцам, а по средним — у взрослого мужчины это около 176 см.
4. Верста (изначально около 750 саженей) — эта древнерусская единица означала, сколько пройдет плуг при пахоте до очередного поворота. Верста со временем изменилось: при Алексее Михайловиче в нее помещалось уже до 1000 саженей, а при Петре I сохранилось всего 500 (1060-1070 м). “Петровской” межевой верстой измеряли расстояние между дорожными столбами. Она существовала вплоть до введения метрической системы.

С XV в. в измерительной системе начинаются изменения: вместо локтя появились аршин (16 вершков, от кончиков пальцев вытянутой руки до плеча, около 71 см) и вершок (ширина двух пальцев, примерно 4,5 см), а размер официальной сажени в 1649 году приравняли к трем аршинам. Во избежание случаев мошенничества по всей стране были разосланы “официальные” аршины — деревянные плашки, на металлических концах которых было оттиснено государственное клеймо.

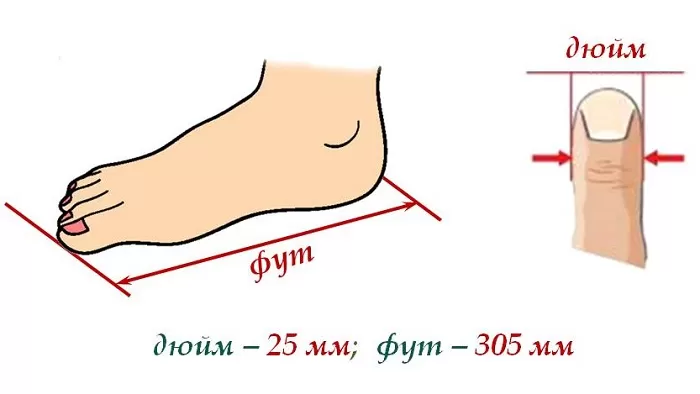
При Петре I возникла необходимость во введении дополнительных мер длины, которые позволят упростить товарооборот между европейскими и отечественными купцами. Так появились фут и дюйм:

• фут — средняя длина ступни, примерно 30,5 см;

• дюйм — ширина большого пальца, чуть больше 2,5 см.

Всего в развитых странах использовалось до 400 единиц измерения: устаревшая классификация серьезно затрудняла торговые и иные отношения, поэтому возникла необходимость в единой системе.

Таблица самых распространенных английских мер измерения

Для удобства основные английские меры измерения сведены в таблицу.

Единица на английском	На русском	Примерное значение
Длина и Площадь (Length & Areas)
mile	миля	1609 м
nautical mile	морская миля	1853м
league	лига	4828,032 м
cable	кабельтов	185,3 м
yard	ярд	0,9144 м
pole, rod, perch	род, поль, перч	5,0292 м
furlong	фарлонг	201,16 м
mil	мил	0,025 мм
line	линия	2,116 мм
hand	хэнд	10,16 см
chain	чейн	20,116 м
point	точка	0,35 мм
inch	дюйм	2,54 см
foot	фут	0,304 м
Square mile	Квадратная миля	258,99 га
Square inch	Кв. дюйм	6,4516 с м²
Square yard	Кв. ярд	0,83613 см²
Square foot	Кв. фут	929,03 см²
Square rod	Кв. род	25,293 см²
acre	акр	4046,86 м²
rood	руд	1011,71 м²
Вес, Масса (Weight)
long ton	тонна большая	907 кг
short ton	тонна малая	1016 кг
chaldron	челдрон	2692,5 кг
pound	фунт	453,59 г
ounce, oz	унция	28,349 г
quintal	квинтал	50,802 кг
short hundredweight	центал	45,36 кг
Hundredweight	Хандредвейт	50,8 кг
tod	тод	12,7 кг
short quarter	квартер короткий	11,34 кг
dram	драхма	1,77 г
grain	гран	64,8 мг
stone	стоун	6,35 кг
Объем (Capacity)
barrel petroleum	баррель нефтяной	158,97 л
barrel	баррель	163,6 л
pint	пинта	0,57 л
bushel	бушель	35,3 л
cubic yard	Кубический ярд	0,76 м³
cubic foot	Куб. фут	0,02 м³
cubic inch	Куб. дюйм	16,3 см³
liquid ounce	Жидкая унция	28,4 мл
quart	кварта	1,136 л
gallon	галлон	4,54 л
Melchizedek	Мелхиседек	30 л
Primat	Примат	27 л
Balthazar	Валтасар	12 л
Methuselah	Мафусаил	6 л
Melchior	Мельхиор	18 л
Jeroboam	Иеровоам	3 л
Magnum	магнум	1,5 л
Rehoboam	Ровоам	4,5 л

Если Вы собрались в путешествие в Англию или Америку, во избежание неловких ситуаций ознакомьтесь с местным стандартом мер. Для этого не обязательно заучивать цифры. В случае необходимости можно воспользоваться конвертером.

Меры жидких и сыпучих тел

Основные меры:

Баррель (англ. barrel — бочка) — мера объёма сыпучих веществ и жидкостей, равная «бочке». Используется для измерения объёма в экономических расчётах и в некоторых странах.

Для измерения объёма сыпучих веществ существовал так называемый «английский баррель»: 1 английский баррель = 4,5 бушеля = 163,66 литра. В США стандартный баррель для жидкости равен 31,5 американских галлонов, то есть: 1 американский баррель = 31,5 американских галлонов = 119,2 литров = 1/2 хогсхеда.

Однако при измерении объёма пива (из-за налоговых ограничений) в США используется так называемый стандартный пивной баррель, который равен 31 американскому галлону (117,3 литров).

Также в США используется единица, именуемая «сухой баррель» (dry barrel), которая равна 105 сухим квартам (115,6 литра).

Для наиболее часто употребляемого в мире понятия барреля (а именно, для нефти) имеется особая мера, отличная от всех перечисленных (Баррель нефтяной).

1 Нефтяной баррель = 158,987 литра. Международное обозначение: bbls.

Бушель (англ. bushel) — единица объёма, используемая в английской системе мер. Применяется для измерения сыпучих товаров, в основном сельскохозяйственных, но не для жидкостей. Сокращённо обозначается bsh. или bu.

В британской имперской системе мер для сыпучих тел: 1 бушель = 4 пекам = 8 галлонам = 32 сухим квартам = 64 сухим пинтам = 1,032 американским бушелям = 2219,36 кубическим дюймам = 36,36872 л (дм³) = 3 вёдрам.

В американской системе мер для сыпучих тел: 1 бушель = 0,9689 английских бушеля = 35,2393 л; по другим данным: 1 бушель = 35,23907017 л = 9,309177489 американских галлонов.

Кроме того, бушелем называют тару для хранения и транспортировки яблок. В международной торговле под бушелем, как правило, понимается коробка весом 18 кг.

Галлон (англ. gallon) — мера объёма в английской системе мер, соответствующая от 3,79 до 4,55 литра (в зависимости от страны употребления). Обычно используется для жидкостей, в редких случаях — для твёрдых тел. Дольные единицы галлона — пинта и унция. Американский галлон равен 3,785411784 литра. Галлон изначально определялся как объём 8 фунтов пшеницы. Пинта является производной величиной от галлона — одна восьмая его часть. Позже другие разновидности галлона были введены в обиход для других продуктов и, соответственно, появились новые варианты пинт. Америка приняла британский винный галлон, определённый в 1707 году как 231 кубический дюйм, в качестве основной меры объёма жидкости. Отсюда была выведена американская жидкая пинта. Был также принят британский кукурузный галлон (268,8 кубического дюйма) как мера объёма сыпучих тел. Отсюда произошла американская сухая пинта. В 1824 годубританский парламент заменил все варианты галлона на один имперский галлон, определённый как 10 фунтов дистиллированной воды при температуре 62 °F (277,42 кубического дюйма).

Американский галлон и английский галлон различаются:

•        американский галлон ≈ 3,785 литра;
•        английский галлон = 4,5461 литра.

В США стандартный баррель для жидкости равен 42 американским галлонам, то есть: 1 американский баррель = 42 американских галлона = 159 литров = 1/2 хогсхеда. Однако при измерении объёма пива (из-за налоговых ограничений) в США используется так называемый стандартный пивной баррель, который равен 31 американскому галлону (117,3 литра).

Унция (лат. uncia) — название нескольких единиц измерения массы, а также двух мер объёма жидких тел, одной единицы измерения силы и нескольких денежных единиц, образованных как двенадцатая доля другой единицы. Термин происходит ещё из древнего Рима, где унцией обозначали двенадцатую часть либры. Являлась одной из основных весовых единиц средневековой Европы. На сегодняшний день применяется при торговле драгоценными металлами — тройская унция, а также в странах, где вес измеряется в фунтах (например, США). Кварта (англ. quart от лат. quartus — четверть) — единица объёма, применяемая в США, Великобритании и других странах для измерения сыпучих или жидких объёмов, равная четверти галлона.

• 1 кварта = 2 пинты = 1/4 галлона.
• 1 американская сухая кварта = 1,1012209 л.
• 1 американская кварта для жидкостей = 0,9463 л.
• 1 английская имперская кварта = 1,1365 л.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

• 1 тонна = 10 центнеров;
• 1 центнер = 100 килограмм;
• 1 килограмм = 1000 грамм;
• 1 грамм = 1000 миллиграмм.

Меры длины:

• 1 километр = 1000 метров;
• 1 метр = 10 дециметров;
• 1 дециметр = 10 сантиметров;
• 1 сантиметр = 10 миллиметров.

Меры площади (квадратные меры):

• 1 кв. километр = 100 гектарам;
• 1 гектар = 10000 кв. метрам;
• 1 кв. метр = 10000 кв. сантиметров;
• 1 кв. сантиметр = 100 кв. миллиметрам.

Меры объёма (кубические меры):

• 1 куб. метр = 1000 куб. дециметров;
• 1 куб. дециметр = 1000 куб. сантиметров;
• 1 куб. сантиметр = 1000 куб. миллиметров.

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).

Меры времени:

• 1 век (столетие) = 100 годам;
• 1 год = 12 месяцам;
• 1 месяц = 30 суткам;
• 1 неделя = 7 суткам;
• 1 сутки = 24 часам;
• 1 час = 60 минутам;
• 1 минута = 60 секундам;
• 1 секунда = 1000 миллисекундам.

Кроме того, используют такие единицы измерения времени, как квартал и декада.

• квартал — 3 месяца;
• декада — 10 суток.

Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь — 31 день. Февраль в простом году — 28 дней, февраль в високосном году — 29 дней. Апрель, июнь, сентябрь, ноябрь — 30 дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый — в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Определение единиц

Размер букв в типографике обозначается словом «кегль». Существует несколько систем измерения кегля, но большинство из них основано на единице «пайка» в американской и английской системе измерения (англ. pica), или «цицеро» в европейской системе измерения. Название «пайка» иногда пишут как «пика». Существуют несколько видов пайки, которые слегка отличаются по величине, поэтому, используя пайку, стоит помнить, какая именно пайка имеется в виду. Изначально в отечественной печати использовали цицеро, но сейчас часто встречается и пайка. Цицеро и компьютерная пайка похожи по величине, но не равны. Иногда цицеро или пайку напрямую используют для измерения, например, чтобы определить размер полей или колонок. Чаще, особенно для измерения текста, используют производные единицы, полученные от пайки, такие как типографские пункты. Размер пайки определяется в разных системах по-разному, как описано ниже.

Буквы измеряют так, как показано на иллюстрации:

Другие единицы

Хотя компьютерная пайка постепенно вытесняет другие единицы, и возможно заменит более привычные цицеро, наряду с ней также используются другие единицы. Одна из таких единиц — американская пайка Она равна 0,166 дюйма или 2.9 миллиметра. Существует еще и типографская пайка . Она равна американской.

В некоторых отечественных типографиях и в литературе о печати до сих пор используют цицеро — единицу, которая широко применялась в Европе (за исключением Англии) до появления компьютерной пайки. Один цицеро равен 1/6 французского дюйма. Французский дюйм немного отличается от современного дюйма. В современных единицах один цицеро равен 4,512 миллиметра или 0,177 дюйма. Эта величина почти равна компьютерным пайкам. Один цицеро — это 1,06 компьютерных пайки.

Круглая шпация (em) и полукруглая шпация (en)

Описанные выше единицы определяют высоту букв, но существуют также единицы, обозначающие ширину букв и символов. Круглая и полукруглая шпации — как раз такие единицы. Первая также известна как кегельная шпация или em, от английского, обозначающего букву M. Ее ширина исторически равнялась ширине этой английской буквы. Аналогично, полукруглая шпация, равная половине круглой — известна под названием en. Сейчас эти величины не определяют с помощью буквы M, так как эта буква может иметь разный размер у разных шрифтов, даже если кегль одинаков.

В русском языке используются короткое и длинное тире. Для обозначения диапазонов и интервалов (например, во фразе: «возьмите 3–4 ложки сахара») используется короткое тире, называемее также тире-en (англ. en dash). Длинное тире используется в русском языке во всех остальных случаях (например, во фразе: «лето было коротким, а зима — длинной»). Оно называется также тире-em (англ. em dash).

Как рассчитать площадь комнаты – пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

Единицы измерения на Руси в XVIII веке

К XVIII веку насчитывалось до 400 различных по величине единиц мер, употребляемых в разных странах. Разнообразие мер затрудняло торговые операции. Поэтому каждое государство стремилось установить единообразные меры для своей страны.

В России, ещё в XVI и XVII вв были определены единые для всей страны системы мер. В XVIII в. в связи с экономическим развитием и необходимостью строгого учёта при внешней торговлей, в России встал вопрос точности измерений, создании эталонов, на основе которых можно было бы организовать поверочное дело (“метрологию”).

Вопрос выбора эталонов из множества существующих (и отечественнных, и “заморских”) оказался непростым. В середине XVIII в. иностранная монета и драгоценные металлы взвешивались в таможнях при поступлении, а затем неоднократно перевешивались на монетных дворах; при этом вес получался различным.

К середине 30-х годов XVIII в. сложилось мнение, что точнее весы в Петербургской тaмoжне. Решено было сделать с таможных весов образцовые, поместить их при Сенате и по ним производить поверку.

Образцом меры длины при определении величины аршина и сажени послужила линейка, принадлежавшая ранее Петру I. На линейке был обозначен полуаршин. По этой полуаршинной мере были изготовлены образцы мер длины – медный аршин и деревянная сажень.

Среди поступивших в Комиссию мер сыпучих тел был выбран четверик Московской большой таможни, по которому осуществлялась поверка мер сыпучих тел других городов.

За основу мер жидкости было принято ведро, присланное из Каменномостского питейного двора в Москве.

В 1736 г. Сенат принял решение об образовании Комиссии весов и мер во главе с главным директором Монетного правления графом Михаилом Гавриловичем Головкиным. Комиссией были созданы образцовые меры – эталоны, установлено отношение различных мер друг к другу, разработан проект организации поверочного дела в стране. Был внесён проект о десятичном построении мер с учётом того, что система русского денежного счета была построена по десятичному принципу.

Определившись с отправными единицами мер, Комиссия приступила к установлению связи между различными единицами измерения при помощи мер длины. Определили объем ведра и четверика. Объем ведра составил 136,297 кубических вершков, а четверика – 286,421 кубических вершков. Итогом работы Комиссии явился «Регламент. »

По аршину, величина которого была определена Комиссией 1736–1742 гг., рекомендовалось в 1745 г. изготовлять «во всем Российском государстве аршины». В соответствии с объемом четверика, принятым Комиссией, во второй половине XVIII в. были изготовлены четверики, полуосьмины и осьмины.

При Павле I указом от 29 апреля 1797 г. об «Учреждении повсеместно в Российской империи верных весов, питейных и хлебных мер» была начата большая работа по упорядочению мер и весов. Завершение ее относится к 30-м годам XIX в. Указ 1797 г. был составлен в форме желательных рекомендаций. Указ касался четырех вопросов измерения: орудий взвешивания, мер веса, мер жидких и сыпучих тел. Как орудия взвешивания, так и все меры подлежали замене, для чего предполагалось отлить чугунные меры.

К 1807 г. были изготовлены три эталона аршина (хранились в Петербурге): хрустальный, стальной и медный. Основанием при определении их величины послужило приведение аршина и сажени к кратному отношению с английск. мерам – в сажени 7 английских футов, в аршине – 28 англ. дюймов. Эталоны были утверждены Александром I и переданы на хранение в Министерство внутренних дел. Для отправки в каждую губернию изготовили 52 медных четырехгранных аршина. Интересно, что до этого, поговорка: «Мерить на свой аршин» – буквально соответствовала реальности. Аршинной мерой продавцы отмеряли длину ткани – оттяжкой от своего плеча.

10 июля 1810 г. Государственный совет России принял решение ввести по всей стране единую меру длины – стандартный 16 вершковый аршин (71,12 см). Казенный клеймлённый аршин ценой 1 рубль серебром приказано было вводить по всем губерниям, с одновременным изъятием старых аршинных шаблонов.

Стадия

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.