Мм² — квадратный миллиметр. конвертер величин

Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Советы и рекомендации

Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.

Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.

Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.

Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.

Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.

Измеряем площадь сложных фигур

Круг и треугольник — сложные формы для самостоятельного расчета. Как измерить квадратные метры круга, если у вас нет математического или инженерного образования? Опять же, применив формулу.

Как измерить размер окружности

Есть формула для вычисления площади круга. Существует постоянное число, отношение длины окружности к ее диаметру. Это число одинаково для всех размеров круга. Он называется пи и равен 3,14. Это число, которое используется в расчетах.

Шаг №1. Измеряем диаметр (это линия, проходящая через центр круга от одного края круга до другого). Пусть диаметр будет 3 м. Затем находим радиус — это половина длины диаметра. Это 1,5 м. Пишем радиус на листе бумаги.

Этап 2. Расчеты производятся по формуле S = RR2, где S — площадь круга, P — фиксированное число, R — радиус круга. Получается 3,14 х (1,5 х 1,5) = 7,065. Площадь этого района составляет 7 065 квадратных метров.

Но это площадь всего круга. Арка над дверью — полукруг. Таким образом, вам все равно придется разделить это число на два, а затем добавить его к прямоугольной области двери. 7.065. 2 = 3,53 м2.

Как измерить площадь треугольника

Если предыдущий хозяин квартиры был математиком, то, возможно, он сделал на потолке треугольные формы, которые нужно восстановить и подчеркнуть другим цветом или штукатуркой. Придется рассчитывать, чтобы не переплачивать.

Вычисление квадрата метра в треугольной фигуре начинается с пристального взгляда на фигуру.

Вам нужно найти основание треугольника, то есть линию, на которой опираются два других (как крыша на домике). Затем проведите линию от противоположной вершины до основания. Запишите эти два числа.

Шаг 1. Основание этого треугольника разделите на 2 и запишите. Этот выпуск нам пригодится в ближайшее время. Измерьте высоту и запишите ее.

Шаг 2. Вычислите площадь этого рисунка. Для этого используйте формулу: S = 0,5ah, где S — площадь треугольника, а — основание, а h — высота. Пример: основание составляет 3 м, а высота — 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Площадь треугольника 3,75 м2. Запишите их, чтобы не забыть о них.

Что такое погонный метр и как его считать

Для чего используют подсчёт погонным метром

Наверное, нет такого человека, который бы ни разу не сталкивался с покупкой мебели и строительных материалов

Делает он это самостоятельно или полагается на продавцов-консультантов — неважно, знать, что означает то или иное понятие не является лишним ни для кого

Соответственно, словосочетание «погонный метр» тоже часто у всех на слуху. Ошибочно множество людей путают его с другим — квадратным метром. Разница известна не каждому.

Погонный метр изначально придумали производители товаров. Как простому потребителю понять сколько чего нужно и какова стоимость, если мастера заказывают материалы в погонных метрах, а магазины указывают стоимость на ценнике в квадратных?

В этой статье приведены объяснения такой терминологии.

На самом деле, понятие погонного метра было придумано для того, чтобы облегчить покупателям стройматериалов жизнь. Чаще всего оно применяется к материалам, которые изготавливаются рулонами: линолеум, ковровые покрытия. Простыми словами — это определение одного метра для материалов с некоторой фиксированной шириной.

Между прочим, рассчитывать необходимую длину и стоимость материала гораздо удобнее именно погонным метром, а не квадратным.Например, возникла необходимость покупки ковровой дорожки на заданную ширину — 3 метра, определенной длины. В таком случае рассчитывать количество квадратных метров будет неуместно, потому что ширина и длина не равноценны, и условно разделить полотно на квадраты не получится.

Это займет время, а также лишние математические расчеты. Попросту говоря, погонным метром называется метр, который знает каждый и значение которого можно рассчитать с помощью метра-рулетки или линейки.

Термин используют также для вычислений, связанных с арматурой. Для этого измеряется длина всех штабелей (в случае если они разной длины) и умножается на вес одного погонного метра. Для вычисления существует специальная таблица, где рассчитывается соотношение в процентах для постройки.

С помощью погонных метров все чаще покупают рулоны пленки для оклеивания теплиц, а также пленку для восстановления кухонных поверхностей. Расчет количества пленки стола такой же, как и для настила пола. А для того чтобы подсчитать количество необходимую для теплицы, изначально надо разбить конструкцию на части, тогда посчитать длину и ширину каждой из них и лишь в конце посчитать погонные метры.

Спектр использования погонного метра широк:

Чем отличается погонный метр от квадратного

Понятие и вычисления квадратного метра известно людям еще со школьных лет. Его применяют для определения площади той или иной фигуры или объекта. Основным отличием от погонного является то, что здесь учитывается именно ширина изделия.

Например, чтобы посчитать необходимое количество линолеума на помещение длиной 4 метра и шириной 3, нужно перемножить эти два показателя – получаем 12 квадратных метров. Этим показателем преимущественно измеряется общая площадь помещения, площадь поверхности, площадь отделочных материалов, площадь с учетом мебели.

Сколько квадратных метров в 1 погонном и наоборот

Часто покупатели материалов сталкиваются с тем, что нужно перевести сколько одной единицы измерения в другой и наоборот. Возможно ли это вычислить, если квадратный метр вычисляет площадь, а погонный — длину? Все гораздо проще, чем кажется на первый взгляд.

Для расчета того же линолеума, делим один погонный метр на ширину изделия, в результате получаем количество квадратных метров.

Часто хозяева попадают в неприятную ситуацию, когда договорились с мастером, который делает им ремонт, на одну цену за выполненную работу, а значит, порядком выше. Споры возникают из-за того, что количество обработанной площади очень отличается от площади, предварительно предусмотренной и оговоренной в смете.

Почему так происходит? Дело в том, что мастера при выполнении тоже пользуются понятием погонного метра. Секрет в том, что мастера называют 1 погонным метром даже ту площадь, длина которой менее 1 метра. Это часто касается работ, связанных с многоуровневыми объектами, потолками и т.д. При отделке, каждый изгиб считается как погонный метр, несмотря на то, что его фактическая длина меньшее.

В таком случае эксперты советуют согласовывать с подрядчиками, в которой единице измерения будет осуществляться расчет. Хотя надо учитывать и то, что обработать ровную без выступов поверхность гораздо сложнее, чем ровную, следовательно, и гораздо затратнее.

Чтобы избежать ошибок в расчетах, в магазин лучше приходить уже с чертежом помещения, на нем должны быть отмечены длина и ширина всех важных для вычисления объектов.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

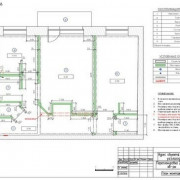
Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Простые геометрические фигуры крыш

Прежде чем выполнять кровельные работы, нужно знать, как рассчитать площадь крыши, чтобы определить, сколько материала потребуется. Его количество всегда нужно брать с запасом и добавлять не менее 10 процентов от общей площади кровли для учета отходов строительства.

Предварительно перед расчетом схему кровли разбивают на простые геометрические фигуры, в нашем примере это две трапеции и два треугольника. Как рассчитать площадь крыши для трапециевидных элементов? Площадь вычисляется по следующей формуле: S=(a+b)xh/2, где: а – ширина нижнего свеса — 10 м, b – ширина по коньку — 7 м, h – высота — 5 м.

Для треугольных элементов применяется формула: S=axh/2, где: а – ширина ската по нижнему свесу — 7 м, h – высота ската — 3 м.

Порядок измерения:

1. Измерить длину, ширину и высоту каждой геометрической фигуры крыши, включая ветровые окна. Эта информация может быть доступна в исходном плане здания дома или, если поверхность крыши относительно низкая и плоская, можно ее измерить самостоятельно. Если хозяин дома сам не может безопасно подняться на крышу, расчет можно выполнить по наружным замерам здания.
2. Перемножить длину и ширину каждой треугольной или трапецеидальной плоскости в отдельности.
3. Вычислить площадь для симметричных треугольных плоскостей, умножив длину основания треугольника (самую длинную сторону) на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
4. Затем разделите итог на 2, чтобы получить результат в квадратных метрах. S=axh/2=7х3/2=10,5 м2.
5. Вычислить площадь для трапеции, умножив ширину нижнего свеса плюс ширину по коньку на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
6. Затем разделить итог на 2, чтобы получить результат в квадратных метрах.
7. Умножить площадь на 0,1, чтобы получить 10-процентную надбавку для запаса кровельного материала S=(a+b)xh/2=(10+7)*5/2= 42,5 м2.
8. Сложить площади всех фигур вместе. S=10,5+10,5+42,5+42,5=106 м2.
9. В результате получается общая площадь крыши 106 м2, с запасом — 116 м2.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Советуем изучить — Какие бывают виды красок для наружных и внутренних работ

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов

В результате получаем площадь пола

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

6 Советы и рекомендации

Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.

Совет! При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.

Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.

Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.

Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.

Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.

Источники

• https://chudopol.ru/raschet-ploshhadi
• https://J.Etagi.com/ps/kak-uznat-ploshchad-komnaty/
• https://stroychik.ru/raznoe/raschet-ploshhadi-i-obema
• https://calcplus.ru/kak-poschitat-ploschad-komnaty/
• https://dolmat.ru/drugoe/kak-rasschitat-kvadraturu-komnaty-osnovnye-metody.html
• https://stroyday.com/kak-poschitat-kvadraturu-komnaty-sten-potolka-pola/
• https://evmaster.net/kalkulyator-ploshhadi-sten
• https://odnushka.ru/steny/ploshchad

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.