Аденокарцинома

Преимущества дифференциации продукта

Дифференцированный продукт может повысить лояльность к бренду и даже пережить более высокую цену. Если продукт воспринимается как лучший, чем его конкуренты, потребители сочтут, что он стоит более высокой цены.

Маркетинг дифференциации может помочь компаниям выделиться, когда продукт не сильно отличается от продукта конкурента, например, воды в бутылках. Стратегия может заключаться в том, чтобы сосредоточиться на более низкой цене или на том, что это местный бизнес. Когда функциональные аспекты двух продуктов идентичны, нефункциональные особенности могут быть выделены. Стратегия может заключаться в простом привлекательном изменении дизайна или стиля.

Краткая справка

Успешная кампания по дифференциации продукта повышает интерес потребителей и дает им основания полагать, что их продукт нужен им по сравнению с другим.

Бесконечномерные многообразия

Представленные здесь многообразия выглядят локально как конечномерные пространства , поэтому эти многообразия конечномерны по определению.
Р.п{\ Displaystyle \ mathbb {R} ^ {п}}

Однако в литературе также есть несколько подходов к определению бесконечно размерных дифференцируемых многообразий. Обычно в определении пространство заменяется локально выпуклым топологическим векторным пространством (так называемым модельным пространством), таким как пространство Фреше , банахово пространство или гильбертово пространство . Затем говорят о локально выпуклых многообразиях, многообразиях Фреше, банаховых многообразиях или гильбертовых многообразиях. Конечно, такое определение имеет смысл только в том случае, если кто-то договорился о том, как определять дифференцируемые и отображения между бесконечномерными локально выпуклыми пространствами. Хотя это относительно некритично для банаховых пространств ( вывод Фреше ), существуют различные, неэквивалентные подходы для любых локально выпуклых пространств.
Р.п{\ Displaystyle \ mathbb {R} ^ {п}}С.k{\ displaystyle C ^ {k}}

Примеры бесконечномерных многообразий:

• единичная сфера в гильбертовом пространстве является -Hilbert многообразия.С.∞{\ Displaystyle C ^ {\ infty}}
• группа унитарных операторов в гильбертовом пространстве является -банаховым многообразием.С.∞{\ Displaystyle C ^ {\ infty}}
• группа диффеоморфизмов на единичной окружности является -Fréchet многообразия.С.∞{\ Displaystyle C ^ {\ infty}}

Как работает дифференциация продуктов

Дифференциация продуктов призвана подтолкнуть потребителя к выбору одного бренда по сравнению с другим среди множества конкурентов. Он определяет качества, которые отличают один продукт от других аналогичных продуктов, и использует эти различия для стимулирования потребительского выбора . Маркетинг дифференциации может также включать сосредоточение внимания на нише рынка. Например, небольшой компании может быть сложно конкурировать с гораздо более крупными конкурентами в той же отрасли. В результате небольшая компания может выделить исключительное обслуживание или гарантию возврата денег.

Этапы дифференциации

Чаще всего используется комплексная дифференциация. То есть компания старается отличаться от конкурентов во всем – и в наборе предлагаемых продуктов, и в их характеристиках, и в качестве обслуживания. Поэтому, как только было решено, за счет чего выделяться, компания должна следовать такому алгоритму:

1. Создать новое название бренда, товара. Оно должно быть запоминающимся, вызывать правильные ассоциации и потребителя.
2. Разработать логотип, упаковку и другие элементы фирменного стиля. Это поможет донести до клиента идею бренда.
3. Персонифицировать бренд или товар, то есть создать живой образ человека, который стоит за продуктом. В качестве персонажа может использовать как реальный прототип – разработчик, первый создатель продукта, так и выдуманный персонаж. В таком случае стоит делать его максимально близким к целевой аудитории, чтобы повысить доверие. 
4. Выпуск товаров с новыми характеристиками и сервисная дифференциация.

Ошибки в проведении

Дифференциация может не принести ожидаемых результатов, если компания неверно выбрала отличительные признаки. Например, продукт компании меньше и компактнее по размеру. Она строит на этом отличии всю рекламную кампанию. Но самим потребителям размеры продукта неважны: при выборе товара, производителя или магазина они основываются на иных критериях. В результате увеличения продаж не происходит.

Как вычислить производную частного двух функций (дробного выражения с функциями)

Определение 5

Данное правило выглядит следующим образом: f(x)g(x)’=f'(x)·g(x)-f(x)·g'(x)g2(x).

Докажем его.  

Доказательство 4

Сразу отметим, что g(x) не будет обращаться в ни при каких значениях x из указанного промежутка. Согласно определению производной, получим:

f(x)g(x)’==lim∆x→∆f(x)g(x)∆x=lim∆x→f(x+∆x)g(x+∆x)-f(x)g(x)∆x=lim∆x→f(x+∆x)·g(x)-g(x+∆x)·f(x)∆x·g(x+∆x)·g(x)==1g2(x)·lim∆x→(f(x)+∆f(x))·g(x)-(g(x)+∆g(x))·f(x)∆x==1g2(x)·lim∆x→f(x)·g(x)+g(x)·∆f(x)-f(x)·g(x)-f(x)·∆g(x)∆x==1g2(x)·lim∆x→gx·∆f(x)-f(x)·∆g(x)∆x==1g2(x)·g(x)·lim∆x→∆f(x)∆x-f(x)·lim∆x→∆g(x)∆x==f'(x)·g(x)-f(x)·g'(x)g2(x)

Пример 9

Продифференцируйте функцию y=sin x2·x+1.

Решение

Эта функция является отношением двух выражений 2x+1 и sin x. Воспользуемся приведенным выше правилом дифференцирования дробного выражения и получим:

y’=sin x2·x+1’=sin x’·2·x+1-sin x·2·x+1’2·x+12

После этого нам потребуется правило для суммы, а также правило вынесения постоянного множителя за знак производной:

y’=sin x’·2·x+1-sin x·2·x+1’2·x+12==cos x·(2·x+1)-sin x·2x’+1′(2·x+1)2=cos x·(2·x+1)-sin x·(2·x’+)(2·x+1)2==cos x·2·x+1-sin x·(2·1·x1-1+)(2·x+1)2=2·x·cos x+cos x-2·sin x(2·x+1)2

Ответ: y’=2·x·cos x+cos x-2·sin x(2·x+1)2

Возьмем задачу на применение всех изученных правил.

Пример 10

Дана функция y=3ex-x2·ln x-2·xax+2sin x·arccos x, где значение undefined является положительным действительным числом. Вычислите производную.

Решение

y’=3·ex’-x2·ln x-2·xax’+2sin x·arccos x’

Поясним, как это получилось.

Первым слагаемым будет 3·ex’=3·ex’=3·ex.

Вычисляем второе:

x2·ln x-2·xax’=x2·ln x-2·x·ax-x2·ln x-2·x·ax’ax2==x2·ln x’-2·x’·ax-x2·ln x-2·x·ax·ln aa2·x==2·x2-1·ln x+x2·1x-2·1·x1-1·ax-x2·ln x-2·x·ax·ln aa2·x==2·x2-1·ln x+x2·1x-2·1·x1-1·ax-x2·ln x-2·x·ax·ln aa2·x==2·x·ln x+x-2·ax-x2·ln x-2·x·ax·ln aa2·x==x·ln x·(2-x·ln a)+x·1-2·ln a-2ax

Вычисляем третье слагаемое:

2sin x·arccos x’=2·sin x·arccos x’==2·sin x’·arccos x+sin x·arccos x’==2·cos x·arccos x-sin x1-x2

Теперь собираем все, что у нас получилось:

y’=3·ex’-x2·ln x-2·xax+2sin x·arccos x’==3·ex-x·ln x·(2-x·ln a)+x·1-2·ln a-2ax++2·cos x·arccos x-sin x1-x2

В задачах, которые мы разобрали в этой статье, использовались только основные элементарные функции, которые были связаны между собой знаками простых арифметических действий. Они нагляднее всего иллюстрируют правила дифференцирования. Однако возможно их применение и к более сложным функциям.

После того, как мы разберем, что такое производная сложной функции, мы сможете проводить дифференцирование выражений любой сложности.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Проведение

Комплексный экзамен проводится в устной или письменной форме и проходит в период зимней или летней сессии, с участием преподавателей, которые вели занятия по включаемым в него дисциплинам.

Во время письменного экзамена в аудитории присутствуют студенты всей группы. Его общая продолжительность, как правило, не превышает двух академических часов.

При сдаче экзамена в устной форме в помещение допускают одновременно не более 5 экзаменуемых. Студенту, который пожелает отвечать первым, предоставляют 20–30 минут для подготовки. В случае затруднения с ответом по выбранному билету, учащийся имеет право вытянуть другой. Время на подготовку ему продлевается, но оценка за экзамен снижается на один балл. Учащемуся, который во время ответа допускает неточности, экзаменатор может задавать дополнительные или уточняющие вопросы.

Иногда преподаватели разрешают студентам пользоваться для подготовки таблицами, наглядными и справочными материалами. А вот брать с собой мобильный телефон и другие средства передачи информации не стоит.

По результатам комплексного экзамена в большинстве учебных заведений выставляют одну общую оценку. Ее же считают оценкой по всем включаемым в него дисциплинам и заносят в соответствующие ведомости.

В целом проведение комплексного экзамена решает сразу нескольких задач. С одной стороны, он дает возможность ограничить число часов промежуточной аттестации, а с другой – проверить целостность восприятия изучаемых дисциплин.

Что такое Дифференциация продукта?

Дифференциация продукта – это маркетинговая стратегия, направленная на выделение продуктов или услуг компании среди конкурентов. Успешная дифференциация продуктов включает выявление и передачу уникальных качеств предложений компании, при этом подчеркивая четкие различия между этими предложениями и другими предложениями на рынке. Дифференциация продукта идет рука об руку с разработкой сильного ценностного предложения, чтобы сделать продукт или услугу привлекательными для целевого рынка или аудитории.

В случае успеха дифференциация продукта может создать конкурентное преимущество для продавца продукта и в конечном итоге повысить узнаваемость бренда. Примеры дифференцированных продуктов могут включать самый быстрый высокоскоростной Интернет или самый экономичный электромобиль на рынке сегодня.

Ключевые моменты

• Дифференциация продукта фокусируется на внимании потребителей к одному или нескольким ключевым преимуществам бренда, которые делают его лучше, чем другие варианты.
• Дифференциация может отражаться в названии, упаковке и продвижении продукта.
• Стратегия дифференциации продукта должна демонстрировать, что продукт может делать все, что могут сделать его конкуренты, но имеет дополнительные преимущества, которые больше не предлагает никто.

Определения

Дифференцируемый атлас

На графике показана замена карт на карты и . Большой круг символизирует топологическое пространство, а два нижних меньших круга символизируют подмножества .(U,ϕ){\ displaystyle (U, \ phi)}(V,ψ){\ displaystyle (V, \ psi)}Р.п{\ Displaystyle \ mathbb {R} ^ {п}}

Карта с топологическим пространством является парой , состоящей из в открытом, непустом множестве и гомеоморфизмеМ.{\ displaystyle M}(U,ϕ){\ displaystyle (U, \ phi)}М.{\ displaystyle M}U⊆М.{\ Displaystyle U \ substeq M}

ϕ U→ϕ(U)⊆Р.п{\ Displaystyle \ phi \ двоеточие \ U \ к \ phi (U) \ substeq \ mathbb {R} ^ {n}}.

Если и две карты с , то фигура называется
(U,ϕ){\ displaystyle (U, \ phi)}(V,ψ){\ displaystyle (V, \ psi)}М.{\ displaystyle M}U∩V≠∅{\ Displaystyle U \ cap V \ neq \ emptyset}

ψ∘ϕ-1 ϕ(U∩V)→ψ(U∩V){\ Displaystyle \ psi \ circ \ phi ^ {- 1} \ двоеточие \ \ phi (U \ cap V) \ to \ psi (U \ cap V)}

изменение карты .

An атлас для затем семейства отображений ( это множество индексов) такие , что
М.{\ displaystyle M}(Uя,ϕя)я∈Я.{\ displaystyle (U_ {я}, \ phi _ {я}) _ {я \ in I}}Я.{\ displaystyle I}

М.знак равно⋃я∈Я.Uя{\ Displaystyle M = \ bigcup _ {я \ in I} U_ {я}}

применяется. Атласе называется -дифференцируем с , если всеми его картой изменений являются -диффеоморфизмами .
С.k{\ displaystyle C ^ {k}}k≥1{\ Displaystyle к \ geq 1}С.k{\ displaystyle C ^ {k}}

Дифференцируемая структура

Два -дифференцируемых атласа эквивалентны , даже если их объединение является -дифференцируемым атласом. Класс эквивалентности атласов в связи с этим отношением эквивалентности называется -дифференцируема структурой коллектора.
С.k{\ displaystyle C ^ {k}}С.k{\ displaystyle C ^ {k}}С.k{\ displaystyle C ^ {k}}

Если да , то также говорят о гладкой структуре .
kзнак равно∞{\ Displaystyle к = \ infty}

Дифференцируемое многообразие

-Time дифференцируемое многообразие является топологическим хаусдорфовым , что удовлетворяет вторую аксиому счетности , вместе с -дифференцируемой структурой.
k{\ displaystyle k}С.k{\ displaystyle C ^ {k}}

Дифференцируемое многообразие имеет размерность, когда карта и, следовательно, все карты отображаются в подмножество .
п{\ displaystyle n}Р.п{\ Displaystyle \ mathbb {R} ^ {п}}

Гладкий коллектор

Гладкое многообразие является также топологическим Хаусдорфово пространство , которое удовлетворяет второй аксиоме счетности, вместе с гладкой структурой.

На гладких многообразиях можно исследовать функции на предмет гладкости , что, конечно, невозможно для многообразий, дифференцируемых по-разам, потому что там изменение отображения дифференцируемо только- раз, и поэтому можно дифференцировать каждую функцию на многообразии только- раз. Часто дифференциальные геометры рассматривают только гладкие многообразия, поскольку для них можно получить примерно те же результаты, что и для однократно дифференцируемых, но не нужно управлять тем, как часто можно еще различать изменения карты.
k{\ displaystyle k}k{\ displaystyle k}k{\ displaystyle k}k{\ displaystyle k}

Понятие логарифмической производной функции

Вычислим производную функции

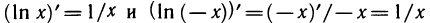
Производная

логарифмической производной функции f(x)

Вычислим с помощью логарифмической производной производную показательно-степенной функции

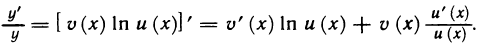
Отсюда, учитывая, что

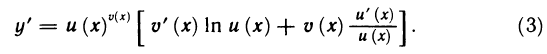
Пример:

Вычислить производную функции

Решение:

Данную функцию можно представить в виде

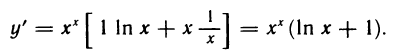
Производную показательно-степенной функции

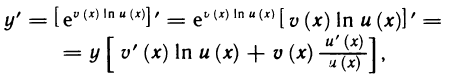
Логарифмическая производная очень удобна при нахождении производной степенной функции с любым вещественным показателем.

Производная степенной функции с любым вещественным показателем

Производная функции

Доказательство:

Так как

Отсюда, учитывая, что

Таким образом, нами вычислены производные всех простейших элементарных функций и мы можем составить следующую таблицу.

Таблица производных простейших элементарных функций

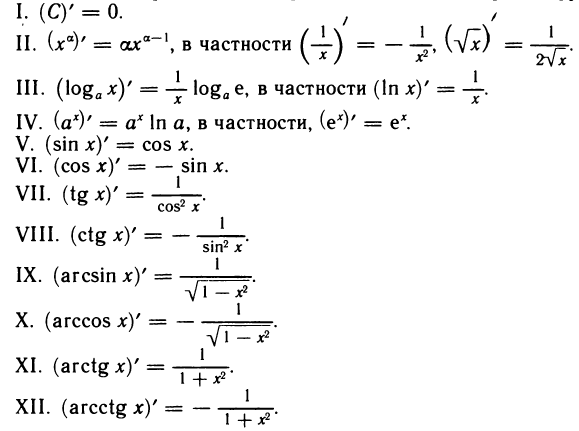
Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.

Симптоматика

На скрытом этапе течения заболевания симптоматика отсутствует.

Первые симптомы появляются из-за разрастания опухоли:

• Боль в той зоне, где локализуется новообразование;
• Наличие сгустков крови;
• Появление запоров;
• Рост лимфатических узлов;
• Потеря в весе;
• Снижение гемоглобина;
• Утомляемость;
• Низкая трудоспособность;
• Плохой сон.

На стадии интенсивного роста раковых клеток и появления метастазов выраженность симптомов усиливается.

Разберем симптоматику при формировании аденокарциномы в различных органах.

Кишечник

• Болезненный живот;
• Неприятные ощущения после приема пищи;
• Плохая проходимость кишечника;
• Жидкий стул, чередующийся с запорами;
• Кровь и слизистые выделения в кале.

Полость носа

• Отек миндалин;
• Не проходящее воспаление миндалин;
• Боли в гортани, глотке, носу;
• Неприятные ощущения при глотании;
• Боль в ушах;
• Нарушение речи;
• Увеличение лимфоузлов.

Как делают КТ средостения?

Для компьютерной томографии используют сложное оборудование. КТ-аппарат состоит из передвижного стола и кольцевой части, внутри которой находятся излучатели и датчики.

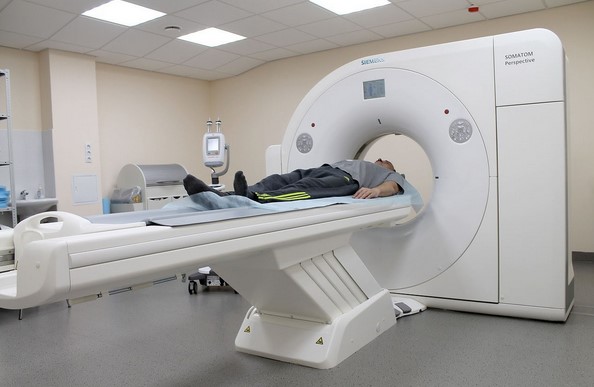
Компьютерная томография легких и органов средостения

Пациент ложится на транспортер лицом вверх. Для повышения качества изображений необходимо соблюдать неподвижность на протяжении всего сеанса. Смена положения тела приводит к искажению картины, появлению артефактов на снимках.

Стол с пациентом перемещается внутри кольца томографа. Сканирующие элементы движутся по кругу, делая за полный оборот несколько снимков. Процедура получила название мультиспиральной компьютерной томографии. МСКТ обеспечивает:

• снижение лучевой нагрузки;

• сокращение времени сканирования;

• повышение качества изображений.

В результате получают фотографии аксиальных срезов, с помощью которых достраивают сагиттальную и фронтальную проекции. Для уточнения локализации патологического очага и оценки взаимного расположения анатомических структур средостения реконструируют 3D-модель рассматриваемой зоны.

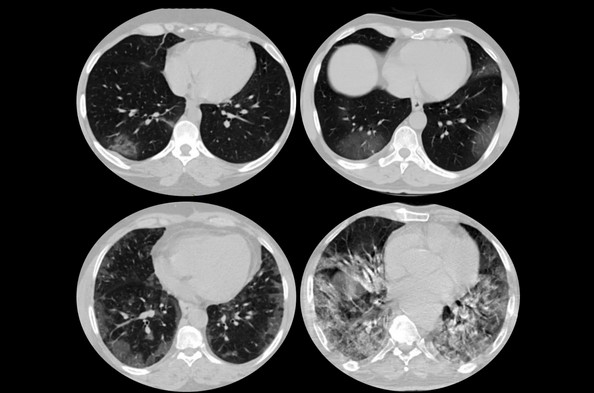
Вирусная (ковидная) пневмония на томограмме

КТ средостения и легких занимает от 5 до 10 минут. При использовании контрастного усиления продолжительность диагностической процедуры увеличивается. Инъекцию делают после серии нативных снимков. Сканирование приостанавливают, через внутривенный катетер пациенту вводят «окрашивающий» раствор. В течение 10-15 минут препарат заполняет просвет сосудов грудной полости, после чего сканирование продолжают.

КТ средостения с контрастом занимает не более получаса. Через 1-2 дня происходит полное очищение организма от следов йодсодержащего раствора.

Прогноз

Для хорошего прогноза нужно диагностировать аденокарциному на начальных стадиях. Если у больного уже есть метастазы, то он будет жить около 4 месяцев, что также будет зависеть от места нахождения очага опухоли.

Если поражен пищевод, то при лечении на первой и второй стадиях заболевания человек живет пять и более лет. При третьей и четвертой степени – смерть в 25% случаях.

Если поражена печень, то больной проживет не более трех лет.

Аденкарцинома – вид ракового заболевания, при котором нужно незамедлительно обратиться к специалисту и провести необходимое лечение в зависимости от вида болезни, локации и степени поражения органа.

Чем отличается лечение высокодифференцированного рака от низкодифференцированного?

Однозначно на этот вопрос ответить не получится, так как рак бывает очень разным

Для одних злокачественных опухолей (например, рак молочной железы, рак простаты) степень дифференцировки имеет особенно важное значение, в случаях с другими онкологическими заболеваниями данный показатель отходит на второй план

В целом можно сказать, что низкодифференцированные опухоли более агрессивны и нуждаются в более агрессивном лечении.

При составлении плана лечения врач-онколог ориентируется на многие показатели: стадию рака, степень дифференцировки, вид и локализацию опухоли, её «молекулярный портрет», состояние здоровья и сопутствующие заболевания пациента. Ранняя диагностика сильно повышает шансы на успешное лечение, но даже в запущенных случаях всегда можно помочь, существенно продлить жизнь пациента.

Запись на консультацию круглосуточно

+7 (495) 151-14-53+7 (861) 238-70-54+7 (812) 604-77-928 800 100 14 98

Зачет и дифференцированный зачет: в чем разница?

Разница между зачетом и дифференцированным зачетом не так уж велика. Основное отличие дифзачета в том, что по результатам его сдачи преподаватель выставляет студенту оценку, а не «зачет»/«не зачет».

В отличие от обычного зачета дифференцированный влияет на размер начисленной стипендии, что автоматически приравнивает его по значимости к экзамену.

Но чем в этом случае зачет с оценкой отличается от экзамена? Во время экзамена студент отвечает по заданному вопросу, и дополнительные ему задают только в случае сомнений или необходимости повысить оценку. В рамках дифференцированного зачета преподаватель имеет право задавать вопросы по всем пройденным материалам в рамках дисциплины.

Это также главное отличие зачета от дифференцированного зачета. Хоть во время зачета студент редко тянет определенный билет, ему все же предлагают отвечать на определенный вопрос, а не «гоняют» по всему курсу.

На самом деле, разница между зачетом и экзаменом не так и велика. Дело в том, что оценка по обоим испытаниям учитывается в дипломе и влияет на размер стипендии

Но иногда отличие зачета с оценкой от экзамена все же есть. В зависимости от требований и целей преподавателя, этот вид оценки знаний может быть промежуточным испытанием.

Например, преподаватель может поставить дифзачет в конце первого семестра, чтобы проверить степень усвоения пройденного материала. А потом, в конце года поставить по этому же предмету экзамен. В этом случае дифзачет преследует многочисленные цели:

• определение уровня пройденного материала;
• выявление степени освоения теоретической и практической части;
• определение степени развитости творческого и образного мышления;
• выявление способности синтезировать знания и уметь применять их на деле.

Рассматривая дифзачет и экзамен, стоит помнить, что экзамен может принимать любой преподаватель (даже тот, которого студент раньше в глаза не видел). Дифзачет же может принимать лишь тот, кто читал курс лекций и проводил семинары по дисциплине.

В зависимости от формы сдачи дифзачета (устная или письменная) преподаватель огласит оценку либо в день сдачи (при устном) или через оговоренный срок (при письменном). В любом случае студент должен узнать оценку до сдачи ведомости в деканат, чтобы у него была возможность оспорить ее и исправить (или уточнить причины именно такой оценки).

Чаще всего дифференцированный зачет назначают после прохождения студенческой практики (учебной или производственной). 

Если вы собираетесь поступать, знание этих особенностей во многом поможет быстрее адаптироваться и даже косвенно повлиять на свою успеваемость. Ну а пока наслаждайтесь первыми днями в университете. А если возникнут вопросы по учебе, сервис студенческой помощи с радостью поможет. 

Как вычислить производную суммы и производную разности

Чтобы доказать второе правило дифференцирования f(x)±g(x)’=f'(x)±g'(x), нам нужно вспомнить определение производной, а также одно из свойств, которым обладает предел непрерывной функции.

Определение 3

f(x)±g(x)’=lim∆x→∆(f(x)±g(x))∆x==lim∆x→fx+∆x±gx+∆x-(f(x)±g(x))∆x==lim∆x→f(x+∆x)-f(x)±(g(x+∆x)-g(x))∆x==lim∆x→f(x+∆x)-f(x)∆x±lim∆x→g(x+∆x)-g(x)∆x==lim∆x→∆f(x)∆x±lim∆x→∆g(x)∆x=f'(x)±g'(x)

Доказательство 2

Так мы можем доказать равенство производной суммы или разности n-ного количества функций сумме или разности их производных:

f1(x)±f2(x)±…±fn(x)’=f1′(x)±f2’±…±fn'(x)

Пример 4

Вычислить производную y=x3+3x+1-ln xln5+3.

Решение

Первым делом упрощаем данную функцию.

y=x3+3x+1-ln xln5+3=x3+3·3x-ln(5+3)·ln x

После этого применяем второе правило – производной суммы/разности:

y’=(x3)’+3·3x’-ln5+3·ln x’

Первое правило говорит нам о том, что можно вынести постоянный множитель за знак производной, значит:

y’=(x3)’+3·3x’-ln5+3·ln x’==(x3)’+3·3x’-ln(5+3)·ln x’

Нам остается только заглянуть в таблицу производных и взять оттуда соответствующее значение:

y’=(x3)’+3·3x’-ln(5+3)·ln x’==3·x3-1+3·3x·ln 3-ln5+3x=3·x2+3x+1·ln 3-ln(5+3)x

Ответ: y’=3·x2+3x+1·ln 3-ln(5+3)x

Формы проведения

Форма проведения такого зачета зачастую зависит от инициативы преподавателя. Он может проводиться в таких форматах, как:

• устный ответ;
• письменная работа.

Итак, что могут представлять из себя подобные формы проведения дифзачета? Если вид его сдачи устный, то это может быть индивидуальный разговор со студентом, когда проверяющий задает ему вопросы по определенным темам, пытаясь оценить общий уровень знаний. Также это может быть коллоквиум, то есть дискуссия или беседа со всеми студентами сразу, по итогам которой некоторые из самых неактивных ее участников могут продолжить сдачу индивидуально.

Письменная форма зачета возможна в виде контрольной работы или творческого проекта. Контрольная работа считается самой оптимальной проверкой знаний, так как позволяет выявить уровень владения материалом наиболее полно и комплексно. Это может быть как тест, так и вопросы для рассуждения на заданные темы.

Может быть предложена и творческая работа: заранее выполнить проект в группах или индивидуально, подготовить презентацию, видео или журнал  — все здесь полностью зависит от фантазии преподавателя или вашей собственной. Зачастую такая форма проверки проводится для оценки результатов практики. Таким образом, преподавателем может быть избран абсолютно любой формат — главное, чтобы он позволял оценить существующий уровень знаний и умений по предмету. В некоторых случаях выбор формы сдачи может быть предоставлен и самим студентам.

Традиционно по билетам, как правило, такой зачет не проводится — по крайней мере, это противоречит его предназначению. Однако на практике иногда происходит иначе, и в таком случае дифзачет фактически представляет собой обыкновенный экзамен — за исключением того, что преподаватель все еще имеет право проверить ваши знания по другим темам.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

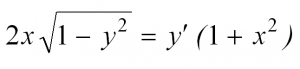
Сначала  перепишем производную в более привычном виде:

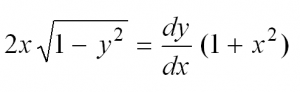
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

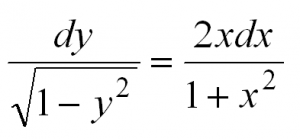
Теперь осталось проинтегрировать обе части:

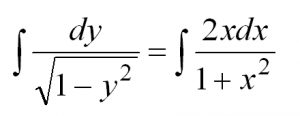
Интегрируем и получаем общее решение данного уравнения:

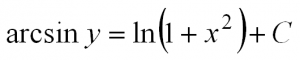
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Физический смысл производной

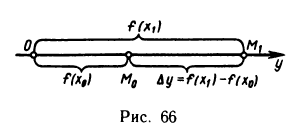
Предположим, что функция y=f(x) описывает закон движения материальной точки М по прямой линии, т. е. y=f(х) — путь, пройденный точкой М от начала отсчета за время х.

Тогда за время

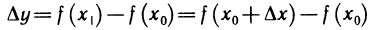
Отношение

Понятие скорости, заимствованное из физики, удобно при исследовании поведения произвольной функции. Какую бы зависимость ни отражала функция y=f(x), отношение

Значение производной состоит в том, что при изучении любых процессов и явлений природы с ее помощью можно оценить скорость изменения связанных между собой величин.

Правая и левая производные

Используя понятие правого и левого предела функции, введем понятия правой и левой произ-в0дных функции у=f(х) в точке

Определение:

Правой (левой) производной функции y=f(x) в точке

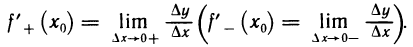
Если функция f(х) имеет в точке

Вместе с тем существуют функции, имеющие в данной точке

Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.

Теорема:

Для того чтобы функция y=f(x) была дифференцируема в точке

Доказательство:

Необходимость. Пусть функция у=f(х) дифференцируема в точке

Переходя к пределу при

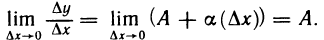
Дх—О Лх Лх-0

Отсюда следует, что производная в точке

Достаточность. Пусть существует конечная производная

где

Таким образом, для функций одной переменной дифференци-руемость и существование производной — понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.

Замечание. Введенная при доказательстве достаточности функция